Algoritmo di Dijkstra

Template:Avvisounicode

Disambiguazione – Se stai cercando l'algoritmo per la mutua esclusione in sistemi concorrenti, detto anche "algoritmo di proiezione di Dijkstra", vedi la voce algoritmo di Dekker.

Algoritmo di Dijkstra
Esecuzione dell'algoritmo di Dijkstra
Classe	Algoritmo di ricerca
Struttura dati	Grafo
Caso peggiore temporalmente	${\displaystyle O(|E|+|V|\log |V|)}$[1]

L'algoritmo di Dijkstra è un algoritmo utilizzato per cercare i cammini minimi in un grafo con o senza ordinamento, ciclico e con pesi non negativi sugli archi. Fu inventato nel 1956 dall'informatico olandese Edsger Dijkstra che lo pubblicò successivamente nel 1959. Tale algoritmo trova applicazione in molteplici contesti quale l'ottimizzazione nella realizzazioni di reti (idriche, telecomunicazioni, stradali, circuitali, ecc.) o l'organizzazione e la valutazione di percorsi runtime nel campo della robotica.

Algoritmo

Supponiamo di avere un grafo con n vertici contraddistinti da numeri interi {1,2,...,n} e che 1 sia scelto come nodo di partenza. Il peso sull'arco che congiunge i nodi j e k è indicato con p(j,k). Ad ogni nodo, al termine dell'analisi, devono essere associate due etichette, f(i) che indica il peso totale del cammino (la somma dei pesi sugli archi percorsi per arrivare al nodo i-esimo) e J(i) che indica il nodo che precede i nel cammino minimo. Inoltre definiamo due insiemi S e T che contengono rispettivamente i nodi a cui sono già state assegnate le etichette e quelli ancora da scandire.

1. Inizializzazione.
   • Poniamo S={1}, T={2,3,...,n}, f(1)=0, J(1)=0.
   • Poniamo f(i)=p(1,i), J(i)=1 per tutti i nodi adiacenti ad 1.
   • Poniamo f(i)= ∞, per tutti gli altri nodi.
2. Assegnazione etichetta permanente
   • Se f(i)= ∞ per ogni i in T STOP
   • Troviamo j in T tale che f(j)=min f(i) con i appartenente a T
   • Poniamo T=T${\displaystyle \setminus }$ {j} e S=S∪{j}
   • Se T=Ø STOP
3. Assegnazione etichetta provvisoria
   • Per ogni i in T, adiacente a j e tale che f(i)>f(j)+p(j,i) poniamo:
     • f(i)=f(j)+p(j,i)
     • J(i)=j
   • Andiamo al passo 2

Pseudocodice

Nel seguente algoritmo, il codice u := vertici in Q con la più breve dist[], cerca per dei vertici u nell'insieme dei vertici Q che hanno il valore dist[u] più piccolo. Questi vertici sono rimossi dall'insieme Q e restituiti all'utente. dist_between(u, v) calcola la distanza tra due nodi vicini u e v. La variabile alt nelle linee 20 22 rappresenta la lunghezza del percorso dal nodo iniziale al nodo vicino v se passa da u. Se questo percorso è più corto dell'ultimo percorso registrato per v, allora il percorso corrente è rimpiazzato dal percorso identificato con alt. L'array precedente è popolato con un puntatore al nodo successivo del grafo sorgente per ricevere il percorso più breve dalla sorgente.

 1  function Dijkstra(Grafo, sorgente):
 2      For each vertice v in Grafo:                               // Inizializzazione
 3          dist[v] := infinito ;                                  // Distanza iniziale sconosciuta 
 4                                                                 // dalla sorgente a v
 5          precedente[v] := non definita ;                             // Nodo precedente in un percorso ottimale
 6      end for                                                    // dalla sorgente
 7      
 8      dist[sorgente] := 0 ;                                        // Distanza dalla sorgente alla sorgente
 9      Q := L'insieme di tutti i nodi nel Grafo ;                       // Tutti i nodi nel grafo sono
10                                                                 // Non ottimizzati e quindi stanno in Q
11      while Q non è vuota:                                      // Loop principale
12          u := vertice in Q con la più breve distanza in dist[] ;    // Nodo iniziale per il primo caso
13          rimuovi u da Q ;
14          if dist[u] = infinito:
15              break ;                                            // tutti i vertici rimanenti sono
16          end if                                                 // inaccessibili dal nodo sorgente
17          
18          For each neighbour v di u:                              // dove v non è ancora stato 
19                                                                 // rimosso da Q.
20              alt := dist[u] + dist_tra(u, v) ;
21              if alt < dist[v]:                                  // Rilascia (u,v,a)
22                  dist[v] := alt ;
23                  precedente[v] := u ;
24                  decrease-key v in Q;                           // Riordina v nella coda
25              end if
26          end for
27      end while
28  return dist;

Se siamo interessati solo al percorso minimo tra due vertici sorgente e destinazione, possiamo terminare la ricerca alla riga 13 se u = destinazione. Adesso possiamo leggere il percorso più breve da sorgente a destinazione tramite un'iterazione inversa:

1  S := sequenza vuota
2  u := destinazione
3  while precedente[u] è definito:                                   // Costruisci il cammino minimo con uno stack S
4      inserisci u all'inizio di S                              // Esegui il push del vertice sullo stack
5      u := precedente[u]                                            // Traverse da destinazione a sorgente.
6  end while ;

Adesso la sequenza S è la lista dei vertici che costituiscono un cammino minimo da sorgente a destinazione, o la sequenza vuota se non ci sono percorsi minimi esistenti.

Tempo di esecuzione

Il tempo di esecuzione dell'algoritmo di Dijkstra può essere espresso in funzione di ${\displaystyle |V|}$  e ${\displaystyle |E|}$  ossia, rispettivamente, il numero di vertici e degli archi appartenenti al grafo sul quale viene eseguito. L'algoritmo utilizza una coda di priorità, implementata attraverso un Min-Heap, Max-Heap o un albero Red-Black.

In questo caso dunque il tempo di esecuzione può essere espresso nella forma:

${\displaystyle O{\bigl (}|E|+|V^{2}|{\bigr )}}$ 

Assumendo che il grafo sia generico vale l'approssimazione ${\displaystyle |E|=O(|V^{2}|)}$  e dunque il tempo di esecuzione può essere riscritto come:

${\displaystyle O{\bigl (}|E|+|V^{2}|{\bigr )}=O{\bigl (}|V^{2}|{\bigr )}}$ 

Possiamo quindi concludere affermando che il tempo di esecuzione dell'algoritmo di Dijkstra è proporzionale al quadrato del numero dei vertici appartenenti al grafo sul quale viene eseguito.

Esempio

Alla base di questi problemi c'è lo scopo di trovare il percorso minimo (più corto, più veloce, più economico…) tra due punti, uno di partenza e uno di arrivo. Con il metodo che vedremo è possibile ottenere non solo il percorso minimo tra un punto di partenza e uno di arrivo ma l'albero dei cammini minimi, cioè tutti i percorsi minimi tra un punto di partenza e tutti gli altri punti della rete. Come per praticamente tutti i problemi riguardanti le reti la cosa migliore è fare una schematizzazione della situazione in cui ci troviamo per risolvere l'esercizio più agevolmente ed avere sempre a disposizione i dati necessari. Una buona schematizzazione per i problemi di percorso minimo deve includere tutti i possibili collegamenti tra i nodi (ed i relativi costi) e deve essere fissato un nodo di partenza.

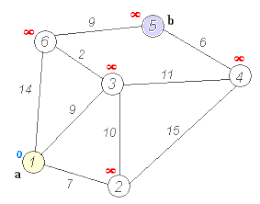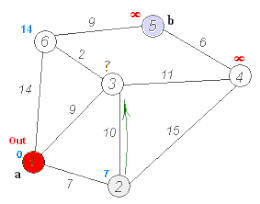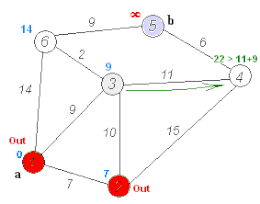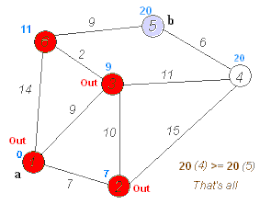
Consideriamo un problema in cui si vuole calcolare il percorso minimo tra casa e il posto di lavoro. Schematizziamo tutti i possibili percorsi ed il relativo tempo di percorrenza (supponendo di voler calcolare il percorso più breve in fatto di tempo di percorrenza). I nodi A, B, C, D, E indicano le cittadine per cui è possibile passare. Ecco una schematizzazione della rete:

 

Dobbiamo ora assegnare ad ogni nodo un valore, che chiameremo “potenziale”, seguendo alcune regole:

• Ogni nodo ha, all'inizio potenziale ${\displaystyle +\infty }$  (che indichiamo con “inf”);
• Il nodo di partenza (in questo caso “casa”) ha potenziale 0 (ovvero dista zero da se stesso);
• Ogni volta si sceglie il nodo con potenziale minore e lo si rende definitivo (colorando il potenziale di rosso) e si aggiornano i nodi adiacenti;
• Il potenziale di un nodo è dato dalla somma del potenziale del nodo precedente + il costo del collegamento;
• Non si aggiornano i potenziali dei nodi resi definitivi;
• I potenziali definitivi indicano la distanza di quel nodo da quello di partenza;
• Quando si aggiorna il potenziale di un nodo si lascia quello minore (essendo un problema di percorso minimo).

Vediamo in pratica come si risolve questo esercizio. Questa è la rete in cui sono indicati anche i potenziali:

 

Seguendo le regole appena fissate consideriamo il nodo con potenziale minore (“casa”) e lo rendiamo definitivo (colorandolo di rosso) ed aggiorniamo tutti i nodi adiacenti sommando l'attuale valore del potenziale (ovvero zero) al costo del percorso. Aggiorniamo i potenziali perché avevamo, nel caso di A, potenziale infinito mentre ora abbiamo potenziale 2. Ricordando che il potenziale minore è sempre preferibile. Vediamo come si è aggiornata la rete:

 

Bisogna ora considerare il nodo non definitivo (ovvero quelli scritti in nero) con potenziale minore (il nodo A). Lo si rende definitivo e si aggiornano i potenziali dei nodi adiacenti B e C. Indichiamo con una freccia da dove proviene il potenziale dei nodi resi definitivi.

 

Il nodo con potenziale minore ora è C. lo si rende definitivo e si aggiornano quelli adiacenti.

 

Va notato come il nodo D abbia ora potenziale 6 in quanto 6 è minore di 8 e quindi lo si aggiorna. Se avessimo avuto un valore maggiore di quello che già c'era lo avremmo lasciato invariato. Rendiamo definitivo il nodo D e aggiorniamo il grafico:

 

Il nodo con potenziale minore restante è B e lo si rende definitivo aggiornando di conseguenza il grafico:

 

Restano da considerare il nodo E e da aggiornare “ufficio”.

 

Seguendo all'indietro le frecce si ottiene il percorso minimo da casa ad ufficio che misura (come indicato dal potenziale) “10”.

 

Bisogna notare come questo algoritmo ci dia non solo la distanza minima tra il punto di partenza e quello di arrivo ma la distanza minima di tutti i nodi da quello di partenza, da cui si può realizzare l'albero dei cammini minimi semplicemente eliminando gli archi non utilizzati da nessun cammino.

Note

1. ^ IEEE Xplore - Fibonacci Heaps And Their Uses In Improved Network Optimization Algorithms

Bibliografia

• Michael T. Goodrich, Roberto Tamassia, Strutture dati e algoritmi in Java, Bologna, Zanichelli Editore, 2007, pp. 556-561, ISBN 978-88-08-07037-1.

Voci correlate

• Algoritmo di Bellman-Ford
• Algoritmo di Prim
• Algoritmo di Kruskal
• Algoritmo di Floyd-Warshall
• PERT/CPM
• Iterative deepening

Altri progetti

Altri progetti

• Wikimedia Commons

•   Wikimedia Commons contiene immagini o altri file su algoritmo di Dijkstra

  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica