Utente:Andrea And/Sandbox/3

Descrizione	Figura	Momento di inerzia	Commento
Massa puntiforme m a distanza r dall'asse di rotazione.		${\displaystyle I=mr^{2}}$	Un massa puntiforme non ha momento di inerzia intorno al proprio asse, ma usando il teorema degli assi paralleli, ###### a moment of inertia around a distant axis of rotation is achieved. #####
Due masse puntiformi, M e m, con massa ridotta ${\displaystyle \mu }$ e separate da una distanza, x.		${\displaystyle I={\frac {Mm}{M\!+\!m}}x^{2}=\mu x^{2}}$	—
Asta di lunghezza L e massa m (Asse di rotazione alla fine dell'asta)		${\displaystyle I_{\mathrm {end} }={\frac {mL^{2}}{3}}\,\!}$  [1]	Questa espressione assume che l'asta sia un filo infinitamente sottile ma rigido. Questo è anche un caso particolare della piastra rettangolare con asse di rotazione alla fine della piastra, e con h = L e w = 0.
Asta di lunghezza L e massa m		${\displaystyle I_{\mathrm {center} }={\frac {mL^{2}}{12}}\,\!}$  [1]	Questa espressione assume che l'asta sia un filo infinitamente sottile ma rigido.Questo è anche un caso particolare della piastra rettangolare con asse di rotazione al centro della piastra, con w = L e h = 0.
Cerchio sottile di raggio r e massa m		${\displaystyle I_{z}=mr^{2}\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!}$	Questo è anche un caso particolare del toro per b = 0. (vedi più in basso.), as well as of a thick-walled cylindrical tube con open ends, con r1=r2 e h = 0.
Disco solido e sottile, di raggio r e massa m		${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{4}}\,\!}$	Questo è un caso particolare del cilindro solido, con h = 0.
Superficie cilindrica sottile con estremità aperte, di raggio r e massa m		${\displaystyle I=mr^{2}\,\!}$  [1]	Questa espressione vale per un cilindro vuoto (come per esempio un tubo), con spessore delle pareti trascurabile (appunto approssimabile a una superficie cilindrica). E' un caso particolare del tubo cilindrico con pareti spesse e r1=r2. Anche una massa puntiforme (m) alla fine di un'asta di lunghezza r ha lo stesso momento di inerzia, e il valore r è chiamato raggio di inerzia.
Cilindro solido di raggio r, altezza h e massa m		${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$  [1] ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)}$	Questo è un caso particolare del tubo cilindrico con pareti spesse, con r1=0. (Nota: in questa immagine gli assi X-Y sono scambiati rispetto agli assi cartesiani standard)
Tubo cilindrico con pareti spesse, di raggio interno r1, raggio esterno r2, lunghezza h e massa m		${\displaystyle I_{z}={\frac {1}{2}}m\left({r_{1}}^{2}+{r_{2}}^{2}\right)}$  [1][2] ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{2}}^{2}+{r_{1}}^{2}\right)+h^{2}\right]}$ o definendo lo spessore normalizzato tn = t/r e ####### r = r2, allora ${\displaystyle I_{z}=mr^{2}\left(1-t_{n}+{\frac {1}{2}}{t_{n}}^{2}\right)}$	con densità ρ e la stessa geometria ${\displaystyle I_{z}={\frac {1}{2}}\pi \rho h\left({r_{2}}^{4}-{r_{1}}^{4}\right)}$ ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}\pi \rho h\left(3({r_{2}}^{4}-{r_{1}}^{4})+h^{2}({r_{2}}^{2}-{r_{1}}^{2})\right)}$
Sfera (cava) di raggio r e massa m		${\displaystyle I={\frac {2mr^{2}}{3}}\,\!}$  [1]	Una sfera cava può essere considerata come costituita da due pile di cerchi infinitamente sottili, uno sopra l'altro, con i raggi che aumentano da 0 a r (o un'unica pila, con il raggio dei cerchi crescente da -r a r).
Sfera (piena) di raggio r e massa m		${\displaystyle I={\frac {2mr^{2}}{5}}\,\!}$  [1]	Una sfera può essere considerata come costituita da due pile di dischi solidi infinitamente sottili, uno sopra l'altro, con i raggi che aumentano da 0 a r (o un'unica pila, con il raggio dei cerchi crescente da -r a r). Un altro modo per ottenere la sfera piena è considerarla costituita da sfere cave infinitamente sottili, con raggio crescente da 0 a r.
Cono circolare retto con raggio r, altezza h e massa m		${\displaystyle I_{z}={\frac {3}{10}}mr^{2}\,\!}$  [3] ${\displaystyle I_{x}=I_{y}={\frac {3}{5}}m\left({\frac {r^{2}}{4}}+h^{2}\right)\,\!}$  [3]	—
Toro con raggio ###del tubo## a, raggio ###trasversale###b e massa m.		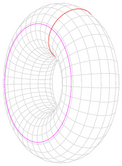About a diameter: ${\displaystyle {\frac {1}{8}}\left(4a^{2}+5b^{2}\right)m}$  [4] About the vertical axis: ${\displaystyle \left(a^{2}+{\frac {3}{4}}b^{2}\right)m}$  [4]	—
Ellipsoid (solid) of semiaxes a, b, e c con axis of rotation a e massa m		${\displaystyle I_{a}={\frac {m(b^{2}+c^{2})}{5}}\,\!}$	—
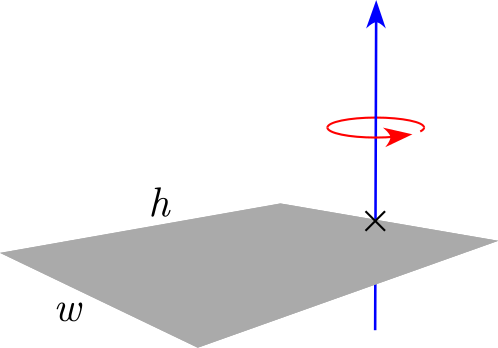
Piastra rettangolare sottile di altezza h, larghezza w e massa m (Axis of rotation at the end of the plate)		${\displaystyle I_{e}={\frac {mh^{2}}{3}}+{\frac {mw^{2}}{12}}\,\!}$	—
Piastra rettangolare sottile di altezza h, larghezza w e massa m		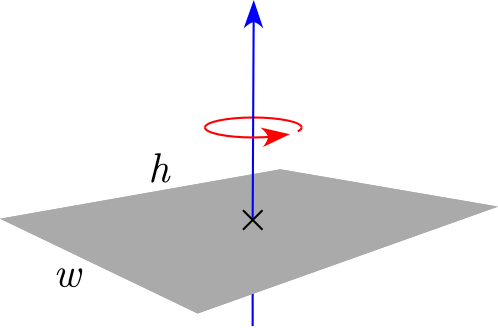${\displaystyle I_{c}={\frac {m(h^{2}+w^{2})}{12}}\,\!}$  [1]	—
Parallelepipedo solido di altezza h, larghezza w, profondità d e massa m		${\displaystyle I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)}$ ${\displaystyle I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)}$ ${\displaystyle I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)}$	Per un cubo orientato allo stesso modo e con lati di lunghezza ${\displaystyle s}$: ${\displaystyle I_{CM}={\frac {ms^{2}}{6}}\,\!}$.
Parallelepipedo solido di altezza D, larghezza W, lunghezza L e massa m con asse lungo la diagonale più lunga.		${\displaystyle I={\frac {m\left(W^{2}D^{2}+L^{2}D^{2}+L^{2}W^{2}\right)}{6\left(L^{2}+W^{2}+D^{2}\right)}}}$	Per un cubo di lato ${\displaystyle s}$, ${\displaystyle I={\frac {ms^{2}}{6}}\,\!}$.
Poligono piano con vertici ${\displaystyle {\vec {P}}_{1}}$, ${\displaystyle {\vec {P}}_{2}}$, ${\displaystyle {\vec {P}}_{3}}$, ..., ${\displaystyle {\vec {P}}_{N}}$ e massa ${\displaystyle m}$ uniformemente distribuita, che ruota intorno a un asse perpendicolare al piano e passante per l'origine.		${\displaystyle I={\frac {m}{6}}{\frac {\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|(({\vec {P}}_{n+1}\cdot {\vec {P}}_{n+1})+({\vec {P}}_{n+1}\cdot {\vec {P}}_{n})+({\vec {P}}_{n}\cdot {\vec {P}}_{n}))}{\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|}}}$	Questa espressione assume che il poligono sia ####star-shaped####. I vettori ${\displaystyle {\vec {P}}_{1}}$, ${\displaystyle {\vec {P}}_{2}}$, ${\displaystyle {\vec {P}}_{3}}$, ..., ${\displaystyle {\vec {P}}_{N}}$ sono i vettori posizione dei vertici.
Disco infinito con massa distribuita normalmente su due assi intorno all'asse di rotazione (per esempio: ${\displaystyle \rho (x,y)={\tfrac {m}{2\pi ab}}\,e^{-((x/a)^{2}+(y/b)^{2})/2}}$ dove ${\displaystyle \rho (x,y)}$ è la densità della massa in funzione di x e y).		${\displaystyle I=m(a^{2}+b^{2})\,\!}$	—

Vedi anche

• Momento di inerzia
• Teorema di Huygens-Steiner, o degli assi paralleli

Note

1. Raymond A. Serway, Physics for Scientists e Engineers, second ed., Saunders College Publishing, 1986, p. 202, ISBN 0-03-004534-7.
2. ^ Classical Mechanics - Moment of inertia of a uniform hollow cylinder. LivePhysics.com. Retrieved on 2008-01-31.
3. Ferdine P. Beer e E. Russell Johnston, Jr, Vector Mechanics for Engineers, fourth ed., McGraw-Hill, 1984, p. 911, ISBN 0-07-004389-2.
4. Eric W. Weisstein, Moment of Inertia — Ring, su scienceworld.wolfram.com, Wolfram Research. URL consultato il 25 marzo 2010.