In category theory, a branch of mathematics, the pullback (also called the fiber product) is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain.
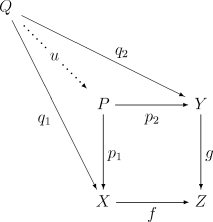
Explicitly, the pullback of the morphisms f and g consists of an object P and two morphisms p1 : P → X and p2 : P → Y for which the diagram
commutes. Moreover, the pullback (P, p1, p2) must be universal with respect to this diagram. That is, for any other such set (Q, q1, q2) there must exist a unique u : Q → P making the following diagram commute:
As with all universal constructions, the pullback, if it exists, is unique up to a unique isomorphism.
The pullback is often written
- P = X ×Z Y.
The notation comes from the following example. In the category of sets the pullback of f and g is the set
- X ×Z Y = {(x, y) ∈ X × Y | f(x) = g(y)}
The maps p1 and p2 are just the projections onto the first and second factors.
This example motivates another way of characterizing the pullback: as the equalizer of the morphisms f O p1, g O p2 : X × Y → Z where X × Y is the binary product of X and Y and p1,2 are the natural projections. This shows that pullbacks exist in any category with binary products and equalizers.
The categorical dual of a pullback is a called a pushout.