Quicksort

Quicksort è un ottimo algoritmo di ordinamento ricorsivo in place che, come merge sort, si basa sul paradigma divide et impera. La base del suo funzionamento è l'utilizzo ricorsivo della procedura partition: preso un elemento da una struttura dati (es. array) si pongono gli elementi minori a sinistra rispetto a questo e gli elementi maggiori a destra.

File:Quicksort ordinamento.gif

Quicksort

Un'altra appresentazione grafica dell'algoritmo Quicksort

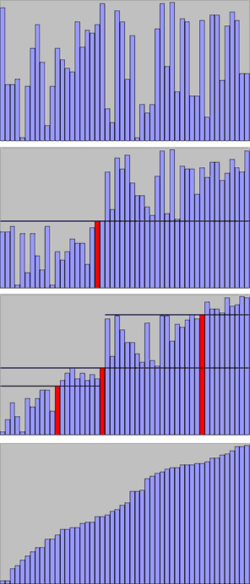
Il Quicksort, termine che tradotto letteralmente in italiano indica ordinamento rapido, è l'algoritmo di ordinamento che ha, in generale, prestazioni migliori tra quelli basati su confronto. È stato ideato da Charles Antony Richard Hoare nel 1960. Il Quicksort è molto popolare dato che è facilmente implementabile ed è un buon algoritmo general purpose, che ha un buon comportamento in un'ampia varietà di situazioni ed in molti casi richiede meno risorse di qualsiasi altro algoritmo. Offre inoltre il vantaggio di operare direttamente sul file da ordinare (utilizzando un piccolo stack ausiliario), e per effettuare l'ordinamento di N elementi richiede mediamente solo ${\displaystyle N\log N\!}$ operazioni e ha un ciclo interno estremamente breve. Gli svantaggi sono dati dal fatto che non è stabile, nel caso peggiore ha un comportamento quadratico ed è particolarmente fragile: un semplice errore nella sua implementazione può passare inosservato ma causare in certe situazioni un drastico peggioramento nelle prestazioni dell'algoritmo.

Il Quicksort è stato sottoposto a un'analisi matematica approfondita ed estremamente precisa, tanto che le sue prestazioni sono state comprese a fondo e il suo comportamento è stato descritto in modo molto accurato. I risultati ottenuti in fase di analisi sono stati verificati sperimentalmente in modo esteso e l'algoritmo di base è stato migliorato al punto da diventare il metodo ideale per un gran numero di applicazioni pratiche.

Sono stati svolti inoltre numerosi studi per migliorare le prestazioni anche in considerazione del fatto che la ricerca di un algoritmo di ordinamento più veloce è una delle principali attrattive dell'informatica. Praticamente dal momento in cui Hoare pubblicò per la prima volta il suo lavoro, la letteratura specializzata iniziò a proporre versioni migliorate dell'algoritmo. Sono state provate e analizzate molte idee, ma l'algoritmo è così ben bilanciato da far si che il miglioramento apportato in una parte del programma quasi inevitabilmente dia luogo a un peggioramento delle prestazioni in qualche altro punto.

Per la sua estrema facilità è stato scelto in molte librerie di linguaggi come il C di implementare di base una funzione che effettui l'ordinamento del Quicksort. C'è da tenere presente che spesso ci si può sorprendere del comportamento indesiderato e inatteso in presenza di input particolari, specialmente se si tratta di versioni dell'algoritmo messe a punto accuratamente. Se un'applicazione non giustifica il lavoro necessario ad assicurare che l'implementazione del Quicksort sia esente da errori lo Shell sort rappresenta una scelta sicura in grado di garantire prestazioni sufficientemente buone a fronte di un minore sforzo implementativo.

Algoritmo di Base

L'idea base può esprimersi agevolmente in termini ricorsivi. Ad ogni stadio si effettua un ordinamento parziale di una sequenza di oggetti da ordinare. Assunto un elemento come perno dello stadio, si confrontano con esso gli altri elementi e si posizionano alla sua sinistra i minori e a destra i maggiori, senza tener conto del loro ordine. Dopo questo stadio si ha che il perno è nella sua posizione definitiva.

Successivamente si organizzano nuovi stadi simili nei quali si procede all'ordinamento parziale delle sottosequenze di elementi rimasti non ordinati, fino al loro esaurimento.

Lo pseudocodice per il Quicksort è:

Template:Matematica voce

C'è da notare che la partition è la funzione più discussa dagli studiosi. In molte versioni inizia la scelta del perno in modo casuale. Quindi effettua una scansione degli elementi dalla sinistra saltando quelli più piccoli e dalla destra saltando quelli più grandi, scambiando gli elementi che arrestano le scansioni e continuando fino a che i puntatori utilizzati per la scansione si incrociano. La scansione partita da sinistra si ferma una volta incontrato l'elemento perno, mentre quella partita da destra si interrompe quando arriva al carattere precedente al perno. Questo ciclo continua e l'ultima operazione da effettuare consiste nell'invertire le posizioni degli ultimi elementi che hanno interrotto la scansione.

Specifica dell'algoritmo

 

Animazione dell'algoritmo

Si vuole fornire una versione più dettagliata dell'algoritmo che specifichi la struttura dati utilizzata e il processo di partizione. L'obiettivo è quello di implementare la procedura mediante un procedimento che calcoli la sequenza ordinata attraverso scambi diretti tra i valori delle sue componenti, senza usare vettori aggiuntivi per mantenere risultati parziali della computazione. In questo modo lo spazio di memoria utilizzato è essenzialmente ridotto alle celle necessarie per mantenere il vettore di ingresso e per implementare la ricorsione.

Si rappresenta la sequenza di input mediante il vettore ${\displaystyle A=(A[1],A[2],...A[n])\,\,n\geq 1}$  componenti. Per ogni coppia di interni p,q tali che ${\displaystyle 1\leq p\leq q\leq n}$  denotiamo ${\displaystyle A_{p,q}=(A[p],A[p+1],...A[q])}$  . Il cuore dell'algoritmo è costituto dalla funzione che partiziona l'insieme, per comodità chiamiamo Partition(p,q). Questa procedura ripartisce gli elementi del vettore ${\displaystyle A_{p,q}}$  rispetto al valore ${\displaystyle \alpha }$  della prima componente ${\displaystyle A[p]}$ ; questa funzione modifica quindi il valore delle componenti di ${\displaystyle A_{p,q}}$  e restituisce un indice ${\displaystyle l\in [p,p+1,...q]}$  che gode delle seguenti proprietà:

1. ${\displaystyle A[l]}$  assume il valore ${\displaystyle \alpha }$ 
2. ${\displaystyle A_{p,l-1}}$  contiene i valori minori o uguali ad ${\displaystyle \alpha }$  originariamente contenti in ${\displaystyle A_{p+1,q}}$ 
3. ${\displaystyle A_{l,q}}$  contiene i valori maggiori di ${\displaystyle \alpha }$  originariamente contenuti in ${\displaystyle A_{p+1,q}}$ 

La funzione partition può essere calcolata dalla seguente procedura nella quale due puntatori scorrono il vettore da destra a sinistra e viceversa confrontando le componenti con l'elemento scelto casualmente. Per impedire ad uno dei due puntatori di uscire dall'insieme dei valori ammissibili aggiungiamo una sentinella al vettore A, cioè una componente ${\displaystyle A[n+1]}$  che assume un valore convenzionale superiore a quello di tutti gli elementi di A.

Supponiamo inoltre che il parametro A rappresenti una variabile globale; per questo motivo gli unici parametri formali della procedura sono p e q che rappresentano gli indici del sottovettore sul quale si opera la partizione (assumiamo sempre ${\displaystyle 1\leq p\leq q\leq n}$ ). Le altre variabili che compaiono nella procedura sono locali.

Template:Matematica voce

Rianalizzando l'algoritmo del quicksort prima esposto si comprende che la funzione partition è il fulcro delle operazioni.

Analisi delle prestazioni

Caso peggiore

Denotiamo con ${\displaystyle T_{w}(n)}$  il massimo numero di confronti tra elementi del vettore di ingresso eseguiti dall'algoritmo su input A di lunghezza n. È evidente che i vettori A1 e A2 della partizione possono essere calcolati mediante n-1 confronti (dato che un elemento viene scelto come pivot). Inoltre la dimensione di A1 e A2 è data rispettivamente da k e n-k-1, per qualche ${\displaystyle k\in [0,1,...,n-1]}$ . Questo implica che per ogni ${\displaystyle n\geq 1}$ :

${\displaystyle T_{w}(n)=n-1+max_{0\leq k\leq n-1}{T_{w}(k)+T_{w}(n-k-1)}}$ 

mentre per n = 0

${\displaystyle T_{w}(0)=0}$ . Questa è l'equazione di ricorrenza per l'algoritmo in questione. Si vuole ora determinare il ${\displaystyle T_{w}(0)}$  esatto. Nel caso pratico questo valore sarà utile per capire il comportamento dell'algoritmo nel caso in cui si sceglie l'elemento massimo o minimo per il partizionamento (il caso peggiore). Infatti poiche ${\displaystyle max_{0\leq k\leq n-1}[T_{w}(k)+T_{w}(n-k-1)]\geq T_{w}(n-1)}$  abbiamo che ${\displaystyle T_{w}(n)\geq n-1+T_{w}(n-1)}$  e quindi per ogni ${\displaystyle n\in N}$  otteniamo:

${\displaystyle T_{w}(n)=\sum _{0}{n-1}k={\frac {n(n-1)}{2}}}$ .

In questo modo abbiamo ottenuto che l'algoritmo nel caso peggiore ha un costo quadratico. Il caso peggiore si verifica quando lo sbilanciamento è totale, cioè quando l'algoritmo di partizionamento restituisce una partizione di lunghezza n-1 e una di lunghezza 0; in questo caso il tempo di esecuzione è Θ(${\displaystyle n^{2}}$ ).

Raffinamento dell'algoritmo per ottenere come caso peggiore O(nlogn).

Vogliamo evitare che la scelta del partizionamento ci conduca ad un tempo quadratico. Per fare questo è sufficiente scegliere l'elemento mediano della sequenza. La selezione del mediano può essere fatta tramite l'algoritmo QuickSelect, il che ci consente di trovarci sempre ad avere una sequenza di al più parte_intera_superiore(n/2) elementi, ovvero ad avere un tempo asintotico pari a O(nlogn) nel caso peggiore. Ad una analisi più accurata, tuttavia, si verifica che la costante moltiplicativa è circa 24 (e non 1.39, come nel caso migliore). Per accorgersene è sufficiente scegliere il pivot seguendo questi passi: - Costruire n/5 quintuple: l'ultimo sottoarray può non essere una quintupla (ma un insieme più piccolo) - Per ogni quintupla calcolare il mediano, effettuanto in totale, 7n/5 confronti, perché il mediano di 5 elementi può essere calcolato con al più 7 confronti. - Ricavare un campione, ottenuto come mediano dei mediani delle quintuple - Calcolare il pivot come mediano dei mediani, impiegando un tempo pari a T(n/5) (chiamata ricorsiva) 5. Partiziona intorno al pivot: (n-1) confronti (ovvio) 6. Prosegui ricorsivamente: T( (7/10) n ) (perché la chiamata viene effettuata un insieme con cardinalità pari, al più 7n/10 +3).

L'equazione di ricorrenza diventa:

T(n) ≤ (12/5) n + T( n/5 ) + T( (7/10) n )

che ha soluzione O(n), in particolare T(n)<=cn <-> c>24.

Caso medio

Per lo studio nel caso medio si valuta il numero medio di confronti tra elementi del vettore di ingresso eseguiti dall'algoritmo, determinando di conseguenza l'ordine di grandezza del tempo medio di calcolo necessario per eseguire la procedura.

Caso migliore

Il caso migliore si verifica quando l'algoritmo di partizionamento determina due sottoproblemi perfettamente bilanciati, entrambi di dimensione n/2; in questo caso il tempo di esecuzione è Θ(nlogn), precisamente 1.39NlogN.

Dimensione dello stack

L'algoritmo utilizza la ricorsione che in casi di anomalie potrebbe portare a problemi di STACK OVERFLOW. È possibile operare un processo di rimozione della ricorsione senza alterare le prestazioni utilizzano un stack esterno che memorizza il "lavoro da fare" in forma di file parziali da ordinare. Ogni qualvolta si richiede un sottofile da ordinare è sufficiente estrarlo dalla stack mentre in seguito a un partizionamento i due file parziali generati possono essere inseritivi. Nell'implementazione ricorsiva (quelle viste sopra), lo stack viene gestito dal sistema contiene le stesse informazioni che si salveranno in questo stack esterno. Per un fle casuale la massima dimensione dello stack è proporzionale a ${\displaystyle \log n}$  anche se in casi degeneri lo stack può crescere proporzinalmente a N. Il caso peggiore è quello in cui il file risulta già ordinato. Questo problema è tanto sottile quanto reale: anche un programma ricorsivo utilizza (implicitamente ) uno stack, per cui la degenerazione del quicksort per file di grandi dimensioni potrebbe casuare una terminazione anomala del programma per mancanza di memoria disponibile. Ovviamente un comportamento del genere deve essere evitato soprattutto se si vuole inserire la routine in una libreria di programma. Non è facile dare garanzie che ciò non avvenga anche se non è difficile fare in modo che questi casi degeneri siano estramente improbabili.

Per effettuare lo studio della dimensione dello stack si effettua la valutazione dello spazio di memoria necessario alla procedura del quicksort. Oltre alle n celle necessarie per contenere il vettore dei valori di ingresso, occorre utilizzare una certa quantità di spazio per mantenere la pila che implementa la ricorsione. Nel caso peggiore Quicksort(1,n) utilizza uno spazio ${\displaystyle O(n)}$  per mantenere la pila. Se infatti viene estratto l'elemento maggiore del campione, la pila deve conservare i parametri relativi a un massimo di n - 1 chiamate ricorsive.

Quicksort iterativo

Il primo passaggio da fare per passare dalla strategia ricorsiva a quella iterativa è quello di inserire il più grande dei due sottofile da ordinare nello stack assicurando che ogni sottofile presente nello stack non sia più grande della metà di quello che gli sta sotto, quindi lo stack non dovrà contenere più di un numero logaritmico di oggetti. Questa dimensione massima dello stack si verifica quando il partizionamento è effettuato sempre al centro del file. Per file casuali l'occupazione di stack è verosimilmente piccola.

La versione di base del quicksort potrà essere migliorare modificando appositamente le chiamate ricorsive. Più precisamente si può forzare la procedura ad eseguire sempre la prima chiamata relativa al sottovettore di lunghezza minore. Si ottiene un nuovo algoritmo con le seguenti istruzioni (la procedura viene scritta in pseudocodice)

Template:Matematica voce A questo punto è possibile operare la trasformazione e passare nella versione iterativa. Si osserva innanzitutto che in questo caso il criterio di gestione della pila può essere semplificato sfruttando il fatto che le due chiamate ricorsive sono le ultime istruzioni della procedura. Si può quindi definire una versione iterativa nella quale la pila serve per mantenre l'elenco delle chiamate che devono ancora essere eseguite e non sono state neppure iniziate. In altre parole nell'esecuzione della procedura la prima chiamata ricorsiva viene attivata dopo aver accantonato in testa alla pila i parametri necessari per eseguire la seconda. Quest'ultima sarà attivata una volta completata la precedente, quando i suoi parametri si trovano di nuovo in testa alla pila. In particolare non si ha bisogno di mantenere nella pila il record di attivazione della procedura (che qualsiasi linguaggio di programmazione fa ogni qual volta viene chiamata una procedura).

L'algoritmo così ottenuto è descritto dalla seguente procedura: Template:Matematica voce Si può dimostrare che la procedura è corretta. Infatti al termine dell'esecuzione di ogni ciclo repeat-until le parti del vettore di ingresso non ancora ordinate sono contenute nella pila S oppure in A_p,q. La verifica di questa proprietà è facile. Di conseguenza quando si esce dal ciclo la condizione S <> NULL E q - p < 1 garantisce che il vettore di ingresso sia ordinato.

Valutazione altezza massima dello stack

Si osserva innanzitutto che il vettore A_p,q sul quale la macchina sta lavorando non è mai maggiore del vettore che si trova in testa alla pila S. Inoltre, ad ogni incremento di S la dimensione A_p,q, viene ridotta almento della metà. Quindi durante la computazione la pila può contenere al più ${\displaystyle log_{2}N}$  elementi dove n è la dimensione dell'input.

Quicksort misto ricorsivo-iterativo

Come descritto per il Quicksort iterativo, anche per questa strategia il primo passo è quello di modificare la procedura ricorsiva considerando il fatto che la seconda chiamata alla funzione Quicksot avviene alla fine della procedura, quando non c'è più quindi la necessità di mantenere nello stack le informazioni e lo stato della funzione chiamante. Si può allora trasformare la seconda chiamata ricorsiva in un loop interno alla funzione chiamante stessa, dopo averne opportunamente aggiornato i parametri d'ingresso. Se a questo primo passo aggiungiamo che la prima chiamata ricorsiva non la effettuiamo a caso, ma sulla parte di vettore da ordinare che risulta più corta (e quindi mai maggiore della metà del vettore di partenza), otteniamo contemporaneamente una strategia che: riduce il numero di chiamate ricorsive, utilizza lo stack di sistema senza doverne creare uno ad hoc, limita la profondità massima dello stack, anche nel caso peggiore, a ${\displaystyle log_{2}N}$  elementi.

Si riporta una efficiente implementazione in C della strategia descritta. Il codice può essere compilato per ordinare stringhe, numeri interi, etc.

Template:Matematica voce

File parziali di piccole dimensioni

Partizionamento con il metodo della mediana

Il metodo della mediana di 3 è un tipico approccio che consente di migliorare i partizionamenti dell'array, evitando partizioni troppo sbilanciate, e consiste nell'effettuare il partizionamento scegliendo opportunamente il pivot nel sottoarray: in particolare si sceglie come pivot la mediana di un insieme di tre elementi selezionati a caso dal sottoarray.

Chiavi duplicate

Stringhe e vettori

Selezione

Implementazioni

Seguono alcuni esempi di implementazione in vari linguaggi.

C

Template:Matematica voce //attenzione, il programma non è completo!

C++

Template:Matematica voce

Haskell

Template:Matematica voce

Java

Questo esempio mostra un quicksort generico, piuttosto che uno che funzioni con gli interi o con le stringhe. Template:Matematica voce

Joy

Template:Matematica voce

Lisp

Template:Matematica voce

Pascal

Template:Matematica voce

Perl

Template:Matematica voce

Perl 6

Template:Matematica voce

Python

Template:Matematica voce

Prolog

Template:Matematica voce

Ruby

Template:Matematica voce

SML

Template:Matematica voce

Bibliografia

• Hoare, C. A. R. (1961): Partition: Algorithm 63, Quicksort: Algorithm 64, and Find: Algorithm 65., Comm. ACM 4, pp. 321-322
• Sedgewick, Robert (1978): Implementing quicksort programs, Communications of the ACM, 21(10) pp. 847-857.
• Musser, David (1997): Introspective Sorting and Selection Algorithms, Software Practice and Experience vol 27, number 8, pp. 983-993
• LaMarca, A.; Ladner, R. E. (1997): The Influence of Caches on the Performance of Sorting, Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 370-379.

Voci correlate

• qsort - Funzione presente nella libreria standard del C che implementa l'algoritmo di ordinamento quicksort.

Collegamenti esterni

• Interactive quicksort
• Multidimensional quicksort in Java
• Video spiegazione di Quicksort usando le schede e del codice in C++