The rectangular function (also known as the rectangle function , rect function , unit pulse , or the normalized boxcar function :
Rectangular function
r
e
c
t
(
t
)
=
⊓
(
t
)
=
{
0
if
|
t
|
>
1
2
1
2
if
|
t
|
=
1
2
1
if
|
t
|
<
1
2
.
{\displaystyle \mathrm {rect} (t)=\sqcap (t)={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|t|<{\frac {1}{2}}.\end{cases}}}
Alternate definitions of the function define
r
e
c
t
(
±
1
2
)
{\displaystyle \mathrm {rect} (\pm {\begin{matrix}{\frac {1}{2}}\end{matrix}})}
Heaviside step function ,
u
(
t
)
{\displaystyle u(t)}
:
r
e
c
t
(
t
τ
)
=
u
(
t
+
τ
2
)
−
u
(
t
−
τ
2
)
,
{\displaystyle \mathrm {rect} \left({\frac {t}{\tau }}\right)=u\left(t+{\frac {\tau }{2}}\right)-u\left(t-{\frac {\tau }{2}}\right),\,}
or, alternatively:
r
e
c
t
(
t
)
=
u
(
t
+
1
2
)
⋅
u
(
1
2
−
t
)
.
{\displaystyle \mathrm {rect} (t)=u\left(t+{\frac {1}{2}}\right)\cdot u\left({\frac {1}{2}}-t\right).\,}
The unitary Fourier transforms of the rectangular function are:
∫
−
∞
∞
r
e
c
t
(
t
)
⋅
e
−
i
2
π
f
t
d
t
=
sin
(
π
f
)
π
f
=
s
i
n
c
(
f
)
,
{\displaystyle \int _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i2\pi ft}\,dt={\frac {\sin(\pi f)}{\pi f}}=\mathrm {sinc} (f),\,}
and:
1
2
π
∫
−
∞
∞
r
e
c
t
(
t
)
⋅
e
−
i
ω
t
d
t
=
1
2
π
⋅
s
i
n
c
(
ω
2
π
)
,
{\displaystyle {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i\omega t}\,dt={\frac {1}{\sqrt {2\pi }}}\cdot \mathrm {sinc} \left({\frac {\omega }{2\pi }}\right),\,}
where
s
i
n
c
{\displaystyle \mathrm {sinc} }
We can define the triangular function as the convolution of two rectangular functions:
t
r
i
(
t
)
=
r
e
c
t
(
t
)
∗
r
e
c
t
(
t
)
.
{\displaystyle \mathrm {tri} (t)=\mathrm {rect} (t)*\mathrm {rect} (t).\,}
Viewing the rectangular function as a probability distribution function, its characteristic function is:
φ
(
k
)
=
sin
(
k
/
2
)
k
/
2
,
{\displaystyle \varphi (k)={\frac {\sin(k/2)}{k/2}},\,}
and its moment generating function is:
M
(
k
)
=
s
i
n
h
(
k
/
2
)
k
/
2
,
{\displaystyle M(k)={\frac {\mathrm {sinh} (k/2)}{k/2}},\,}
where
s
i
n
h
(
t
)
{\displaystyle \mathrm {sinh} (t)}
hyperbolic sine function.
See also 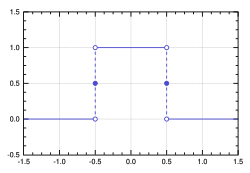
![{\displaystyle \mathrm {rect} (t)=\sqcap (t)={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|t|<{\frac {1}{2}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f245b8e1ae2b29983b6d85b3d3338ef53f1bae07)










