Exponential-logarithmic distribution

Template:Wikify is deprecated. Please use a more specific cleanup template as listed in the documentation.

In probability theory and statistics, the Exponential-Logarithmic (EL) distribution is a family of lifetime distribution with
decreasing failure rate, defined on the interval ${\displaystyle (0,\infty )}$. This distribution is parameterized by two parameters ${\displaystyle p\in (0,1)}$ and ${\displaystyle \beta >0}$.

Exponential-Logarithmic distribution (EL)

Probability density function
Hazard function
Parameters	${\displaystyle p\in (0,1)}$ ${\displaystyle \beta >0}$
Support	${\displaystyle x\in (0,infty)}$
Probability density function (pdf)	${\displaystyle {\frac {1}{-\ln p}}\times {\frac {\beta (1-p)e^{-\beta x}}{1-(1-p)e^{-\beta x}}}}$
Cumulative distribution function (cdf)	${\displaystyle 1-{\frac {\ln(1-(1-p)e^{-\beta x})}{\ln p}}}$
Mean	${\displaystyle -{\frac {polylog(2,1-p)}{\beta \ln p}}}$
Median	${\displaystyle {\frac {\ln(1+{\sqrt {p}})}{\beta }}}$
Mode	0
Variance	${\displaystyle -{\frac {2polylog(3,1-p)}{\beta ^{2}\ln p}}-{\frac {polylog^{2}(2,1-p)}{\beta ^{2}\ln ^{2}p}}}$
Skewness
Excess kurtosis
Moment-generating function (mgf)	${\displaystyle -{\frac {\beta (1-p)}{\ln p(\beta -t)}}}$ ${\displaystyle hypergeom_{2,1}([1,{\frac {\beta -t}{\beta }}],[{\frac {2\beta -t}{\beta }}],1-p)}$
Characteristic function

[table of contents]

Introduction

The study of length of organisms, devices, materials, etc., is of major importance in the biological and engineering science. In general, life time of an device is expected to exhibit decreasing failure rate (DFR) when its behavior over time is characterized by 'work-hardening' (in engineering term) or 'immunity' (in biological term).

The Exponential-Logarithmic model together with its various properties are studied in Tahmasbi and Rezaei (2008)^[1] This model is obtained under the concept of population heterogeneity (through the process of compounding).

Properties of the distribution

Distribution

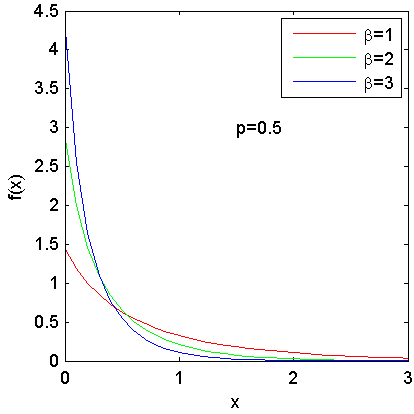
The probability density function of EL distribution is monotone decreasing with modal value ${\displaystyle \beta (1-p)(-p\ln p)^{-1}}$  at ${\displaystyle x=0}$ .

For all values of parameters, the pdf is strictly decreasing in ${\displaystyle x}$  and tending to zero as ${\displaystyle x\rightarrow \infty }$ . The EL leads to exponential distribution with parameter ${\displaystyle \beta }$ , as ${\displaystyle p\rightarrow 1}$ .

The distribution function is given by
${\displaystyle F_{X}(x;p,\beta )=1-{\frac {\ln(1-(1-p)e^{-\beta x})}{\ln p}},}$ 
and hence, the median is obtained by ${\displaystyle {\frac {\ln(1+{\sqrt {p}})}{\beta }}}$ .

Moments

The moment generating function of ${\displaystyle X}$  is determined from pdf by direct integration and is given by ${\displaystyle M_{X}(t)=E(e^{tX})=-{\frac {\beta (1-p)}{\ln p(\beta -t)}}hypergeom_{2,1}([1,{\frac {\beta -t}{\beta }}],[{\frac {2\beta -t}{\beta }}],1-p),}$ 
where ${\displaystyle hypergeom(.)}$  is hypergeometric function. This function is also known as Barnes's extended hypergeometric function. The definition of ${\displaystyle F_{p,q}({n,d},\lambda )}$  is
${\displaystyle F_{p,q}({n,d},\lambda )=\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\prod _{i=1}^{p}\Gamma (n_{i}+k)\Gamma ^{-1}(n_{i})}{\Gamma (k+1)\prod _{i=1}^{q}\Gamma (d_{i}+k)\Gamma ^{-1}(d_{i})}}}$ 
where ${\displaystyle {n}=[n_{1},n_{2},...,n_{p}]}$ , ${\displaystyle p}$  is the number of operands of ${\displaystyle {n}}$ , ${\displaystyle {d}=[d_{1},d_{2},...,d_{q}]}$  and ${\displaystyle q}$  is the number of operands of ${\displaystyle {d}}$ . Generalized hypergeometric function is quickly evaluated and readily available in standard software such as Maple.

The moments of ${\displaystyle X}$  are determined from derivation of ${\displaystyle M_{X}(t)}$ . For ${\displaystyle r\in \mathbb {N} }$ , raw moments are given by
${\displaystyle E(X^{r};p,\beta )=-{\frac {r!polylog(r+1,1-p)}{\beta ^{r}\ln p}},r\in \mathbb {N} ,}$ 
where ${\displaystyle polylog(.)}$  is polylogarithm function and it is defined as follows (Lewin, 1981) ^[2]:
${\displaystyle polylog(a,z)=\sum _{k=1}^{\infty }{\frac {z^{k}}{k^{a}}}.}$ 

Hence the mean and variance of the EL distribution are given, respectively, by
${\displaystyle E(X)=-{\frac {polylog(2,1-p)}{\beta \ln p}},}$ 

${\displaystyle Var(X)=-{\frac {2polylog(3,1-p)}{\beta ^{2}\ln p}}-{\frac {polylog^{2}(2,1-p)}{\beta ^{2}\ln ^{2}p}}.}$ 

The survival, hazard and mean residual life functions

The survival function (also known as reliability function) and hazard function (also known as failure rate function) of the EL distribution are given, respectively, by

${\displaystyle s(x)={\frac {\ln(1-(1-p)e^{-\beta x})}{\ln p}},}$ 

${\displaystyle h(x)={\frac {-\beta (1-p)e^{-\beta x}}{(1-(1-p)e^{-\beta x})\ln(1-(1-p)e^{-\beta x})}}.}$ 

The mean residual lifetime of the EL distribution is given by

${\displaystyle m(x_{0};p,\beta )=E(X-x_{0}|X\geq x_{0};\beta ,p)=-{\frac {\operatorname {dilog} (1-(1-p)e^{-\beta x_{0}})}{\beta \ln(1-(1-p)e^{-\beta x_{0}})}}}$ 

where dilog is dilogarithm function defined as follows:

${\displaystyle \operatorname {dilog} (a)=\int _{1}^{a}{\frac {\ln(x)}{1-x}}\,dx.}$ 

Random number generation

Let ${\displaystyle U}$  be a random variable from standard uniform distribution. Then the following transformation of ${\displaystyle U}$  has EL distribution with parameters ${\displaystyle p}$  and ${\displaystyle \beta }$ :
${\displaystyle X={\frac {1}{\beta }}\ln({\frac {1-p}{1-p^{U}}}).}$ 

Estimation of the parameters

To estimate the parameters, EM algorithm is used. This method is discussed in Tahmasbi and Rezaei (2008). The EM iteration is given by
${\displaystyle \beta ^{(h+1)}=n\{\sum _{i=1}^{n}{\frac {x_{i}}{1-(1-p^{(h)})e^{-\beta ^{(h)}x_{i}}}}\}^{-1},}$ 

${\displaystyle p^{(h+1)}={\frac {-n(1-p^{(h+1)})}{\ln(p^{(h+1)})\sum _{i=1}^{n}\{1-(1-p^{(h)})e^{-\beta ^{(h)}x_{i}}\}^{-1}}}.}$ 

References

1. Tahmasbi, R., Rezaei, S., 2008, "A two-parameter lifetime distribution with decreasing failure rate", Computational Statistics and Data Analysis, Vol. 52, pp. 3889-3901.
2. Lewin, L., 1981, Polylogarithms and Associated Functions, North Holland, Amsterdam.