Parte intera

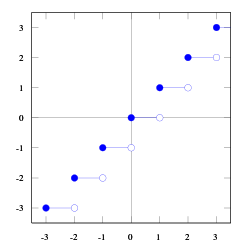
In matematica, la funzione parte intera è la funzione definita come segue: per un numero reale x, la parte intera di x, indicata con int(x) o floor(x) (dalla parola inglese floor che significa "pavimento") è il più grande intero minore od uguale a x. Per esempio int(2.9)=2, int(−2) = −2 e int(−2.3) = −3. La funzione parte intera è anche indicata con ${\displaystyle \lfloor x\rfloor }$ o ${\displaystyle [x]\!}$.

La funzione parte intera

La funzione ${\displaystyle x-\lfloor x\rfloor }$, anche scritta come x mod 1, oppure {x}, è chiamato la parte frazionaria di x. Ogni frazione x può essere scritta come un numero misto, cioè la somma di un intero e una frazione propria. La funzione floor e la funzione parte frazionaria estendono questa decomposizione a tutti i numeri reali.

Qualche proprietà della funzione parte intera

• Si ha

${\displaystyle \lfloor x\rfloor =\max \,\{k\in \mathbb {Z} :k\leq x\}}$

${\displaystyle \lfloor x\rfloor \leq x<\lfloor x\rfloor +1}$

con l'uguaglianza nella parte sinistra che vale se e solo se x è un intero.

• La funzione parte intera è idempotente:

${\displaystyle \lfloor \lfloor x\rfloor \rfloor =\lfloor x\rfloor }$.

• Per ogni intero k e ogni numero reale x,

${\displaystyle \lfloor k+x\rfloor =k+\lfloor x\rfloor .}$

• L'ordinario arrotondamento di un numero x all'intero più vicino può essere espresso come ${\displaystyle \lfloor x+0.5\rfloor }$.
• La funzione parte intera non è continua, ma è semi-continua. Essendo a tratti una funzione costante, la sua derivata è zero quando esiste, cioè per tutti i valori che non sono interi.
• Se x è un numero reale e n un intero, si ha n ≤ x se e solo se n ≤ floor(x). In linguaggio ricercato, la funzione parte intera fa parte di una connessione di Galois; è l'aggiunta superiore della funzione che immerge gli interi nei reali.
• Usando la funzione floor, si possono produrre diverse formule per calcolare i numeri primi che sono esplicite ma non utilizzabili nella pratica.
• Il teorema di Beatty afferma che ogni numero irrazionale partiziona i numeri naturali in due sequenze tramite la funzione floor.

La funzione ceiling (parte intera superiore)

 

La funzione ceiling

Una funzione strettamente correlata alla funzione floor è la funzione ceiling (dalla parola inglese ceiling che significa "soffitto", contrapposta a floor, "pavimento"), definita nel modo seguente: per ogni numero reale x, ceiling(x) è il più piccolo intero non minore di x. Per esempio, ceiling(2.3) = 3, ceiling(2) = 2 e ceiling(−2.3) = −2. La funzione ceiling è anche indicata con ${\displaystyle \lceil x\rceil }$ . È facile provare che

${\displaystyle \lceil x\rceil =-\lfloor -x\rfloor }$ 

e che

${\displaystyle x\leq \lceil x\rceil <x+1}$ 

Per ogni intero k, abbiamo anche che:

${\displaystyle \lfloor k/2\rfloor +\lceil k/2\rceil =k}$ .

Se m e n sono interi positivi primi fra di loro, allora

${\displaystyle \sum _{i=1}^{n-1}\lfloor im/n\rfloor =(m-1)(n-1)/2}$ 

In programmazione

 

L'operatore (int)

In C

Il linguaggio di programmazione C e suoi derivati hanno una caratteristica chiamata conversione di tipo che permette di convertire un valore di un tipo in un valore di un altro tipo. In particolare, è possibile convertire un valore reale (rappresentato in virgola mobile) in un valore intero (rappresentato in complemento a due) applicando l'operatore (int). Questa operazione è un misto delle funzioni floor e ceiling: per x positivi o nulli, restituisce floor(x), e per x negativi resituisce ceiling(x).

Molti altri linguaggi, come Java (testato con Sun JDK versione 1.5.0_05) e Perl (versione 5.8.0) si comportano in maniera simile, così come la funzione POSIX floor().

Problemi di arrotondamento

Come le funzioni floor e ceiling, questa operazione non è continua, cosa che può amplificare gli errori di arrotondamento con conseguenze disastrose. Per esempio (int)(0.6/0.2) restituisce come valore, 2 nella maggior parte delle implementazioni del C, anche se 0.6/0.2 = 3. Questo perché i computer lavorano internamente con il sistema numerico binario e non è possibile rappresentare i numeri 0.6 e 0.2 con stringhe binarie di lunghezza finita. Quindi viene applicato qualche arrotondamento (con il relativo errore) e il risultato viene calcolato come 2.999999999999999555910790149937, che l'operatore (int) convertirà tranquillamente al valore 2.

A causa di questi problemi, la maggior parte delle calcolatrici moderne usa internamente il sistema numerico decimale codificato in binario.

Distribuzione uniforme modulo 1

Se x è un numero irrazionale, allora le parti frazionarie nx mod 1, dove n varia fra gli interi positivi, sono distribuite uniformemente nell'intervallo aperto (0,1). Questa affermazione può essere resa più precisamente in molti modi, uno dei quali afferma:

${\displaystyle \int _{0}^{1}f(t)\;dt=\lim _{N\to \infty }{\frac {1}{N}}\sum _{n=1}^{N}f(nx\;\operatorname {mod} \;1)}$ 

per ogni funzione continua a valori reali ${\displaystyle f:[0,1]\to \mathbb {R} }$  (vedi limite, integrale e teorema dell'equidistribuzione)

Seguendo il principio generale dell'approssimazione diofantina scoperto da Hermann Weyl, questa proprietà è equivalente a qualcosa che è molto più facile da controllare: ovvero che le somme

${\displaystyle \sum \limits _{n=0}^{N}e^{2\pi iknx}}$ 

per ${\displaystyle k\in \mathbb {N} }$  sono O(N). Poiché sono progressioni geometriche, questo può essere provato in maniera abbastanza diretta. La condizione che x sia irrazionale implica che

${\displaystyle \sin \pi kx\neq 0.}$ 

Troncamento

Mentre la funzione parte intera genera solamente numeri interi, il troncamento, cioè il "tagliare fuori le cifre", può essere effettuato a qualsiasi posizione specificata, non solo dopo la cifra delle unità.

Notazione

Le funzioni parte intera superiore e inferiore sono normalmente indicate con parentesi quadre, chiuse e aperte, in cui le linee orizzontali superiori (per la funzione parte intera inferiore, floor) o inferiori (per la funzione parte intera superiore, ceiling) sono mancanti. Per esempio nel sistema di composizione editoriale LaTeX questi simboli possono essere realizzati con i comandi \lfloor, \rfloor, \lceil e \rceil.

  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica