Utente:Andrea And/Sandbox/3
| Descrizione | Figura | Momento di inerzia | Commento |
|---|---|---|---|
| Massa puntiforme m a distanza r dall'asse di rotazione. | — Un massa puntiforme non ha momento di inerzia intorno al proprio asse, ma usando il Parallel axis theorem a moment of inertia around a distant axis of rotation is achieved. | ||
| Due masse puntiformi, M e m, con massa ridotta e separato da una distanza, x. | — | ||
| Rod of length L and mass m (Axis of rotation at the end of the rod) |

|
[1] | This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0. |
| Rod of length L and mass m | 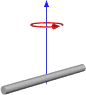
|
[1] | This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with w = L and h = 0. |
| Thin circular hoop of radius r and mass m | 
|
This is a special case of a torus for b=0. (See below.), as well as of a thick-walled cylindrical tube with open ends, with r1=r2 and h=0. | |
| Thin, solid disk of radius r and mass m | 
|
This is a special case of the solid cylinder, with h=0. | |
| Thin cylindrical shell with open ends, of radius r and mass m | 
|
[1] | This expression assumes the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for r1=r2.
Also, a point mass (m) at the end of a rod of length r has this same moment of inertia and the value r is called the radius of gyration. |
| Solid cylinder of radius r, height h and mass m | 
|
[1] |
This is a special case of the thick-walled cylindrical tube, with r1=0. (Note: X-Y axis should be swapped for a standard right handed frame) |
| Thick-walled cylindrical tube with open ends, of inner radius r1, outer radius r2, length h and mass m | 
|
[1][2] or when defining the normalized thickness tn = t/r and letting r = r2, then |
With a density of ρ and the same geometry |
| Sphere (hollow) of radius r and mass m | 
|
[1] | A hollow sphere can be taken to be made up of two stacks of infinitesimally thin, circular hoops, where the radius differs from 0 to r (or a single stack, , where the radius differs from -r to r). |
| Ball (solid) of radius r and mass m | 
|
[1] | A sphere can be taken to be made up of two stacks of infinitesimally thin, solid discs, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).
Also, it can be taken to be made up of infinitesimally thin, hollow spheres, where the radius differs from 0 to r. |
| Right circular cone with radius r, height h and mass m | 
|
[3] [3] |
— |
| Torus of tube radius a, cross-sectional radius b and mass m. | 
|
About a diameter: [4] About the vertical axis: [4] |
— |
| Ellipsoid (solid) of semiaxes a, b, and c with axis of rotation a and mass m | 
|
— | |
| Thin rectangular plate of height h and of width w and mass m (Axis of rotation at the end of the plate) |
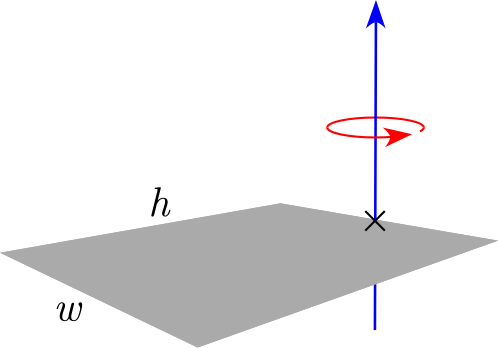
|
— | |
| Thin rectangular plate of height h and of width w and mass m | 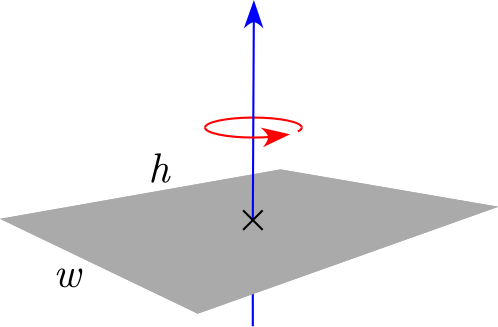
|
[1] | — |
| Solid cuboid of height h, width w, and depth d, and mass m | 
|
For a similarly oriented cube with sides of length , . | |
| Solid cuboid of height D, width W, and length L, and mass m with the longest diagonal as the axis. | 
|
For a cube with sides , . | |
| Plane polygon with vertices , , , ..., and
mass uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin. |

|
This expression assumes that the polygon is star-shaped. The vectors , , , ..., are position vectors of the vertices. | |
| Infinite disk with mass normally distributed on two axes around the axis of rotation
(i.e. Where : is the mass-density as a function of x and y). |

|
— |
See also
References
- ^ a b c d e f g h Raymond A. Serway, Physics for Scientists and Engineers, second ed., Saunders College Publishing, 1986, p. 202, ISBN 0-03-004534-7.
- ^ Classical Mechanics - Moment of inertia of a uniform hollow cylinder. LivePhysics.com. Retrieved on 2008-01-31.
- ^ a b Ferdinand P. Beer and E. Russell Johnston, Jr, Vector Mechanics for Engineers, fourth ed., McGraw-Hill, 1984, p. 911, ISBN 0-07-004389-2.
- ^ a b Eric W. Weisstein, Moment of Inertia — Ring, su scienceworld.wolfram.com, Wolfram Research. URL consultato il 25 marzo 2010.












![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{2}}^{2}+{r_{1}}^{2}\right)+h^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84b03616c2211bce13d6776932c0d56c5b8dabbc)



























