Rectangular function

The rectangular function (also known as the rectangle function, rect function or the normalized boxcar function) is defined as

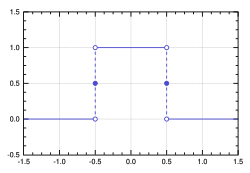Rectangular function

${\displaystyle \mathrm {rect} (x)=\sqcap (x)={\begin{cases}0&{\mbox{if }}|x|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|x|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|x|<{\frac {1}{2}}\end{cases}}}$

or in terms of the Heaviside step function, u(t):

${\displaystyle \mathrm {rect} (x)=u\left(x+{\frac {1}{2}}\right)-u\left(x-{\frac {1}{2}}\right)}$

or, alternatively:

${\displaystyle \mathrm {rect} (x)=u\left(x+{\frac {1}{2}}\right)\cdot u\left({\frac {1}{2}}-x\right)}$

The rectangular function is normalized:

${\displaystyle \int _{-\infty }^{\infty }\mathrm {rect} (x)\,dx=1}$

The unitary Fourier transforms of the rectangular function are:

${\displaystyle {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i\omega t}\,dt={\frac {1}{\sqrt {2\pi }}}\cdot \mathrm {sinc} (\omega /2)}$,   in terms of the unnormalized sinc function.

${\displaystyle \int _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i2\pi ft}\,dt=\mathrm {sinc} (f)}$,   in terms of the normalized sinc function

Viewing the rectangular function as a probability distribution function, its characteristic function is therefore written

${\displaystyle \varphi (k)={\frac {\sin(k/2)}{k/2}}\,}$

and its moment generating function is:

${\displaystyle M(k)={\frac {\mathrm {sinh} (k/2)}{k/2}}\,}$

where "sinh" is the hyperbolic sine function.

See also

• Fourier transform
• Square wave
• Triangular function