The rectangular function (also known as the rectangle function , rect function or the normalized boxcar function
Rectangular function
r
e
c
t
(
x
)
=
⊓
(
x
)
=
{
0
if
|
x
|
>
1
2
1
2
if
|
x
|
=
1
2
1
if
|
x
|
<
1
2
{\displaystyle \mathrm {rect} (x)=\sqcap (x)={\begin{cases}0&{\mbox{if }}|x|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|x|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|x|<{\frac {1}{2}}\end{cases}}}
or in terms of the Heaviside step function , u(t) :
r
e
c
t
(
x
)
=
u
(
x
+
1
2
)
−
u
(
x
−
1
2
)
{\displaystyle \mathrm {rect} (x)=u\left(x+{\frac {1}{2}}\right)-u\left(x-{\frac {1}{2}}\right)}
or, alternatively:
r
e
c
t
(
x
)
=
u
(
x
+
1
2
)
⋅
u
(
1
2
−
x
)
{\displaystyle \mathrm {rect} (x)=u\left(x+{\frac {1}{2}}\right)\cdot u\left({\frac {1}{2}}-x\right)}
The rectangular function is normalized:
∫
−
∞
∞
r
e
c
t
(
x
)
d
x
=
1
{\displaystyle \int _{-\infty }^{\infty }\mathrm {rect} (x)\,dx=1}
The unitary Fourier transforms of the rectangular function are:
1
2
π
∫
−
∞
∞
r
e
c
t
(
t
)
⋅
e
−
i
ω
t
d
t
=
1
2
π
⋅
s
i
n
c
(
ω
2
π
)
{\displaystyle {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i\omega t}\,dt={\frac {1}{\sqrt {2\pi }}}\cdot \mathrm {sinc} \left({\frac {\omega }{2\pi }}\right)}
sinc function .
∫
−
∞
∞
r
e
c
t
(
t
)
⋅
e
−
i
2
π
f
t
d
t
=
s
i
n
c
(
f
)
{\displaystyle \int _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i2\pi ft}\,dt=\mathrm {sinc} (f)}
probability distribution function, its characteristic function is therefore written
φ
(
k
)
=
sin
(
k
/
2
)
k
/
2
{\displaystyle \varphi (k)={\frac {\sin(k/2)}{k/2}}\,}
and its moment generating function is:
M
(
k
)
=
s
i
n
h
(
k
/
2
)
k
/
2
{\displaystyle M(k)={\frac {\mathrm {sinh} (k/2)}{k/2}}\,}
where "sinh" is the hyperbolic sine function.
See also 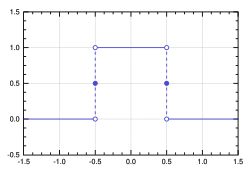
![{\displaystyle \mathrm {rect} (x)=\sqcap (x)={\begin{cases}0&{\mbox{if }}|x|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|x|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|x|<{\frac {1}{2}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18968fc51424e9c28296c1ff41c1164994f55f8c)






