In geometry, a Coxeter-Dynkin diagram is a graph representing a relational set of mirror (or reflectional hyperplanes) in space for a kaleidoscopic construction. Each node in the graph represents one mirror, and each edge represents the dihedral angle between two mirrors.
As a graph itself, the diagram represents Coxeter groups.
The diagram can also represent polytopes by adding rings (circles) around nodes. The rings express information on whether a generating point is on or off the mirror. Specifically a mirror is active (creates reflections) only when points are off the mirror, so adding a ring means a point is off the mirror and creates a reflection.
Edges are labeled with an integer n (or sometimes more generally a rational number p/q) representing a dihedral angle of 180/n. If an edge is unlabeled, it is assumed to be 3. If n is two the angle is 90 degrees and the mirrors have no interaction, and the edge can be left unmarked. Two parallel mirrors can be marked with an infinity (∞) symbol.
In general n mirrors can be represented in an n-simplex graph where all n*(n-1)/2 edges are drawn. In practice interesting sets of mirrors will have a number of right angles, and such edges can be left undrawn.
Polytopes and tessellations can be generating using these mirrors and a single generator point. Mirror images create new points as reflections. Edges can be created between points and a mirror image. Faces can be constructed by cycles of edges created, etc.
Examples:
- A single node represents a single mirror. All points off the mirror are drawn with a ring. Connecting such an off mirror point to its reflection creates a digon or edge perpendicular to the mirror.
- Two unattached nodes represent two perpendicular mirrors. If both nodes are ringed, a rectangle can be created, or a square if the point is equal distance from both mirrors.
- Two nodes attached by an n edge can create an n-gon if the point is on one mirror, and a 2n-gon if the point is off both mirrors.
- Three mirrors in a triangle form images seen in a traditional kaleidoscope and be represented by 3 nodes connected in a triangle. Repeating examples will have edges labeled as (3 3 3), (2 4 4), (2 3 6), although the last two can be drawn in a line with the 2 edge ignored. These will generate uniform tilings.
- Three mirrors with a common point can generate uniform polyhedrons, including rational numbers is the set of Schwarz triangles.
- Three mirrors with one perpendicular to the other two can form the uniform prisms.
In general all regular n-polytopes, represented by Schläfli symbol symbol {p,q,r,...} can have their fundamental domains represented by a set of n mirrors and a related in a Coxeter-Dynkin diagram in a line of nodes and edges labeled by p,q,r...
Examples
- File:Dynkins-100.png - {p,q} - a regular polyhedron or tiling
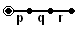- {p,q,r} - a regular polychoron or honeycomb
See also
References
- Coxeter Regular Polytopes (1963), Macmillian Company
- Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Section 11.3 Representation by graphs)
- Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 99-35678 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
External links
 | This geometry-related article is a stub. You can help Wikipedia by expanding it. |