Step function

In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of half-open intervals. Informally speaking, a step function is a piecewise constant function having only finitely many pieces.

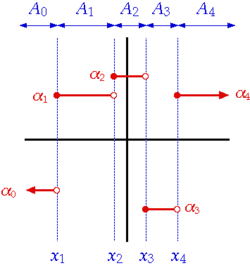
Example of a step function with n=4.

Let the following quantities be given:

• a sequence of coefficients

  ${\displaystyle \{\alpha _{0},\dots ,\alpha _{n}\}\subset \mathbb {R} ,\;n\in \mathbb {N} \setminus \{0\}}$

• a sequence of interval margins

  ${\displaystyle \{x_{1}<\dots <x_{n-1}\}\subset \mathbb {R} }$

• a sequence of intervals

  ${\displaystyle A_{0}:=(-\infty ,x_{1})}$

  ${\displaystyle A_{i}:=[x_{i},x_{i+1})}$ (for ${\displaystyle i=1,\cdots ,n-2}$)

  ${\displaystyle A_{n}:=[x_{n-1},\infty )}$

  (Although the intervals are shown as being closed below and open above, this is not necessary to the definition; all that is required is that the intervals A_n do not intersect, and that their union is the set of real numbers.)

Definition: Given the notations above, a function ${\displaystyle f:\mathbb {R} \rightarrow \mathbb {R} }$ is a step function if and only if it can be written as

${\displaystyle f(x)=\sum \limits _{i=0}^{n}\alpha _{i}\cdot 1_{A_{i}}(x)}$ for all ${\displaystyle x\in \mathbb {R} }$ where ${\displaystyle 1_{A}}$ is the indicator function of ${\displaystyle A}$:

${\displaystyle 1_{A}(x)=\left\{{\begin{matrix}1,&\mathrm {if} \;x\in A\\0,&\mathrm {otherwise} .\end{matrix}}\right.}$

Note: for all ${\displaystyle i=0,\cdots ,n}$ and ${\displaystyle x\in A_{i}}$ it holds: ${\displaystyle f(x)=\alpha _{i}.}$

Special step functions

A version of the unit step function or Heaviside step function, H₁(x), is the special case n=1, α₀=0, α₁=1, and x₁=0.

See also

• simple function
• piecewise defined function