File:VFPt metal balls largesmall transparent.svg

Dimensioni di questa anteprima PNG per questo file SVG: 800 × 600 pixel. Altre risoluzioni: 320 × 240 pixel | 640 × 480 pixel | 1 024 × 768 pixel | 1 280 × 960 pixel | 2 560 × 1 920 pixel.
File originale (file in formato SVG, dimensioni nominali 800 × 600 pixel, dimensione del file: 41 KB)
| Questo file e la sua pagina di descrizione (discussione · modifica) si trovano su Wikimedia Commons (?) |
Dettagli
| DescrizioneVFPt metal balls largesmall transparent.svg |
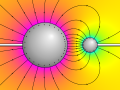
English: Electric field around a large and a small conducting sphere at opposite electric potential. The shape of the field lines is computed exactly, using the method of image charges with an infinite series of charges inside the two spheres, shown in red and blue. In reality, the field is created by a continuous charge distribution at the surface of each sphere and the field lines inside the sphere don't exist. Field lines are always orthogonal to the surface of each sphere. |
| Data | |
| Fonte | Opera propria |
| Autore | Geek3 |
| Altre versioni |
|
| SVG sviluppo InfoField | Questa grafica vettoriale è stata creata con VectorFieldPlot. |
| Codice sorgente InfoField | Python code# paste this code at the end of VectorFieldPlot 1.10
# https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot
u = 100.0
doc = FieldplotDocument('VFPt_metal_balls_largesmall_transparent',
commons=True, width=800, height=600, center=[400, 300], unit=u)
# define two spheres with position, radius and charge
s1 = {'p':sc.array([-1.0, 0.]), 'r':1.5}
s2 = {'p':sc.array([2.0, 0.]), 'r':0.5}
# make charge proportional to capacitance, which is proportional to radius.
s1['q'] = s1['r']
s2['q'] = -s2['r']
d = vabs(s2['p'] - s1['p'])
v12 = (s2['p'] - s1['p']) / d
# compute series of charges https://dx.doi.org/10.2174/1874183500902010032
charges = [[s1['p'][0], s1['p'][1], s1['q']], [s2['p'][0], s2['p'][1], s2['q']]]
r1 = r2 = 0.
q1, q2 = s1['q'], s2['q']
q0 = max(fabs(q1), fabs(q2))
for i in range(10):
q1, q2 = -s1['r'] * q2 / (d - r2), -s2['r'] * q1 / (d - r1),
r1, r2 = s1['r']**2 / (d - r2), s2['r']**2 / (d - r1)
p1, p2 = s1['p'] + r1 * v12, s2['p'] - r2 * v12
charges.append([p1[0], p1[1], q1])
charges.append([p2[0], p2[1], q2])
if max(fabs(q1), fabs(q2)) < 1e-3 * q0:
break
field = Field({'monopoles':charges})
# draw symbols
for c in charges:
doc.draw_charges(Field({'monopoles':[c]}), scale=0.6*sqrt(fabs(c[2])))
gradr = doc.draw_object('linearGradient', {'id':'rod_shade', 'x1':0, 'x2':0,
'y1':0, 'y2':1, 'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#666', 0), ('#ddd', 0.6), ('#fff', 0.7), ('#ccc', 0.75),
('#888', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradr)
gradb = doc.draw_object('radialGradient', {'id':'metal_spot', 'cx':'0.53',
'cy':'0.54', 'r':'0.55', 'fx':'0.65', 'fy':'0.7',
'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#fff', 0), ('#e7e7e7', 0.15), ('#ddd', 0.25),
('#aaa', 0.7), ('#888', 0.9), ('#666', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradb)
ball_charges = []
for ib in range(2):
ball = doc.draw_object('g', {'id':'metal_ball{:}'.format(ib+1),
'transform':'translate({:.3f},{:.3f})'.format(*([s1, s2][ib]['p'])),
'style':'fill:none; stroke:#000;stroke-linecap:square', 'opacity':0.5})
# draw rods
if ib == 0:
x1, x2 = -4.1 - s1['p'][0], -0.9 * s1['r']
else:
x1, x2 = 0.9 * s2['r'], 4.1 - s2['p'][0]
doc.draw_object('rect', {'x':x1, 'width':x2-x1,
'y':-0.1/1.2+0.01, 'height':0.2/1.2-0.02,
'style':'fill:url(#rod_shade); stroke-width:0.02'}, group=ball)
# draw metal balls
doc.draw_object('circle', {'cx':0, 'cy':0, 'r':[s1, s2][ib]['r'],
'style':'fill:url(#metal_spot); stroke-width:0.02'}, group=ball)
ball_charges.append(doc.draw_object('g',
{'style':'stroke-width:0.02'}, group=ball))
# find well-distributed start positions of field lines
def get_startpoint_function(startpath, field):
'''
Given a vector function startpath(t), this will return a new
function such that the scalar parameter t in [0,1] progresses
indirectly proportional to the orthogonal field strength.
'''
def dstartpath(t):
return (startpath(t+1e-6) - startpath(t-1e-6)) / 2e-6
def FieldSum(t0, t1):
return ig.quad(lambda t: sc.absolute(sc.cross(
field.F(startpath(t)), dstartpath(t))), t0, t1)[0]
Ftotal = FieldSum(0, 1)
def startpos(s):
t = op.brentq(lambda t: FieldSum(0, t) / Ftotal - s, 0, 1)
return startpath(t)
return startpos
startp = []
def startpath1(t):
phi = 2. * pi * t
return (sc.array(s2['p']) + 1.5 * sc.array([cos(phi), sin(phi)]))
start_func1 = get_startpoint_function(startpath1, field)
nlines1 = 16
for i in range(nlines1):
startp.append(start_func1((0.5 + i) / nlines1))
def startpath2(t):
phi = 2. * pi * (0.195 + 0.61 * t)
return (sc.array(s1['p']) + 1.5 * sc.array([cos(phi), -sin(phi)]))
start_func2 = get_startpoint_function(startpath2, field)
nlines2 = 14
for i in range(nlines2):
startp.append(start_func2((0.5 + i) / nlines2))
# draw the field lines
for p0 in startp:
line = FieldLine(field, p0, directions='both', maxr=7.)
arrow_d = 2.0
of = [0.5 + s1['r'] / arrow_d, 0.5, 0.5, 0.5 + s2['r'] / arrow_d]
doc.draw_line(line, arrows_style={'dist':arrow_d, 'offsets':of})
doc.write()
|
Licenza
Io, detentore del copyright su quest'opera, dichiaro di pubblicarla con la seguente licenza:
Questo file è disponibile in base alla licenza Creative Commons Attribuzione-Condividi allo stesso modo 4.0 Internazionale
- Tu sei libero:
- di condividere – di copiare, distribuire e trasmettere quest'opera
- di modificare – di adattare l'opera
- Alle seguenti condizioni:
- attribuzione – Devi fornire i crediti appropriati, un collegamento alla licenza e indicare se sono state apportate modifiche. Puoi farlo in qualsiasi modo ragionevole, ma non in alcun modo che suggerisca che il licenziante approvi te o il tuo uso.
- condividi allo stesso modo – Se remixi, trasformi o sviluppi il materiale, devi distribuire i tuoi contributi in base alla stessa licenza o compatibile all'originale.
Didascalie
Aggiungi una brevissima spiegazione di ciò che questo file rappresenta
Elementi ritratti in questo file
raffigura
Valore sconosciuto senza un elemento Wikidata
30 dic 2018
image/svg+xml
Cronologia del file
Fare clic su un gruppo data/ora per vedere il file come si presentava nel momento indicato.
| Data/Ora | Miniatura | Dimensioni | Utente | Commento | |
|---|---|---|---|---|---|
| attuale | 22:05, 30 dic 2018 |  | 800 × 600 (41 KB) | Geek3 | User created page with UploadWizard |
Pagine che usano questo file
Nessuna pagina utilizza questo file.
Utilizzo globale del file
Anche i seguenti wiki usano questo file:
- Usato nelle seguenti pagine di en.wikipedia.org:
- Usato nelle seguenti pagine di es.wikipedia.org:
Metadati
Questo file contiene informazioni aggiuntive, probabilmente aggiunte dalla fotocamera o dallo scanner usati per crearlo o digitalizzarlo. Se il file è stato modificato, alcuni dettagli potrebbero non corrispondere alla realtà.
| Titolo breve | VFPt_metal_balls_largesmall_transparent |
|---|---|
| Descrizione dell'immagine | VFPt_metal_balls_largesmall_transparent
created with VectorFieldPlot 1.10 https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot about: https://commons.wikimedia.org/wiki/File:VFPt_metal_balls_largesmall_transparent.svg rights: Creative Commons Attribution ShareAlike 4.0 |
| Larghezza | 800 |
| Altezza | 600 |