Superellisse

In geometria piana, per superellisse o curva di Lamé si intende una figura geometrica che generalizza l'ellisse. Essa prende il nome da Gabriel Lamé. In un sistema di coordinate cartesiane viene descritto come il luogo dei punti ${\displaystyle (x,y)}$ che soddisfano l'equazione

Un esempio di ipoellisse con ${\displaystyle a=b=1}$ e ${\displaystyle n=1/2.}$

${\displaystyle \left|{\frac {x}{a}}\right|^{n}+\left|{\frac {y}{b}}\right|^{n}=1,}$

con ${\displaystyle n,}$ ${\displaystyle a}$ e ${\displaystyle b}$ reali positivi.

Classificazione

Nel caso ${\displaystyle n=2}$  si ha l'ellisse ordinaria; è inoltre evidente che si tratta di insiemi di punti simmetrici rispetto agli assi ${\displaystyle Ox}$  orizzontale e ${\displaystyle Oy}$  verticale, e quindi anche rispetto al loro punto d'intersezione ${\displaystyle O}$  origine del sistema di riferimento. Per ${\displaystyle n=1}$  si ha un rombo con vertici ${\displaystyle (\pm a,0)}$  e ${\displaystyle (0,\pm b).}$ 

Queste figure si possono ricondurre alle curve della famiglia indicizzata dal solo parametro ${\displaystyle n}$  ottenibili fissando i valori ${\displaystyle a=b=1,}$  cioè alle figure che soddisfano l'equazione normale

${\displaystyle \left|x\right|^{n}+\left|y\right|^{n}=1.}$ 

Una superellisse della forma generale si ottiene applicando a quest'equazione le omotetie ${\displaystyle x\mapsto x/a}$  e ${\displaystyle y\mapsto y/b.}$ 

Osservando le superellissi canoniche si vede che sono invarianti anche per le riflessioni rispetto alle rette per l'origine ${\displaystyle y=x}$  e ${\displaystyle y=-x.}$  Grazie all'invarianza per le riflessioni rispetto ai due assi, i punti di una superellisse si possono ripartire in 4 curve parziali, ciascuna appartenente ad un quadrante. Per studiare le superellissi dunque basta limitarsi al primo quadrante del piano cartesiano e considerare la curva data dalla funzione

${\displaystyle y=(1-x^{n})^{1/n}.}$ 

 

Un esempio di ipoellisse con ${\displaystyle a=b=1}$  e ${\displaystyle n=3/2.}$ 

Altra tipologia di superellisse è quella cuspidale o a "mandorla". Tale tipologia di ellisse possiede tutte le caratteristiche della superellisse classica, ma è discontinua ai vertici arrivando a possedere la caratteristica forma ad "occhio". Alla classe delle superellisse appartengono anche gli ellissoidi ovoidali dalla caratteristica forma ad uovo rappresentabili come delle curve quartiche. Quest'ultima tipologia di superellissi invece è discontinua solo in un punto.

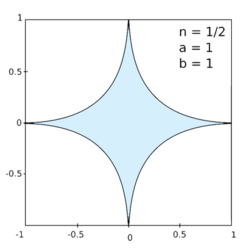
Le figure della famiglia ottenute con ${\displaystyle n>2}$  sono dette iperellissi, quelle relative a ${\displaystyle n<2}$  sono chiamate ipoellissi. All'aumentare di ${\displaystyle n}$  la curva canonica si avvicina sempre di più al rettangolo definito dai vertici opposti ${\displaystyle (1,1)}$  e ${\displaystyle (-1,-1).}$  Al diminuire di ${\displaystyle n}$  da 2 a 1 la curva da cerchio unitario si avvicina al quadrato definito dai vertici opposti ${\displaystyle (1,0)}$  e ${\displaystyle (-1,0).}$  Al diminuire di ${\displaystyle n}$  da 1 a 0 si hanno curve che si avvicinano alla croce formata dai due segmenti di lunghezza 2 con estremità in ${\displaystyle (-1,0)}$  e ${\displaystyle (1,0)}$  e con estremità ${\displaystyle (0,1)}$  e ${\displaystyle (0,-1).}$ 

 

Un esempio di iperellisse con ${\displaystyle a=b=1}$  e ${\displaystyle n=4.}$ 

Bibliografia

• (EN) Martin Gardner, Piet Hein's Superellipse, in Mathematical Carnival, 1992, pp. 240-254.
• Johan Gielis: Inventing the circle. The geometry of nature. - Antwerpen: Geniaal Press, 2003. - ISBN 9080775614
• Cresci Luciano: Le curve matematiche tra curiosità e divertimento - Hoepli 2005

Voci correlate

• Superformula

Altri progetti

Altri progetti

• Wikimedia Commons

•   Wikimedia Commons contiene immagini o altri file su superellisse

Collegamenti esterni

• superellisse, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.  
• (EN) Eric W. Weisstein, Superellipse, su MathWorld, Wolfram Research.  
• Lamé's Super Ellipse (Java-Applet), su activeart.de. URL consultato il 17 settembre 2004 (archiviato dall'url originale il 27 febbraio 2009).
• Super Ellipsoid (Java-Applet), su activeart.de. URL consultato il 17 settembre 2004 (archiviato dall'url originale il 24 maggio 2005).

  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica