Dinatural transformation

In category theory, a branch of mathematics, a dinatural transformation ${\displaystyle \alpha }$ between two functors

${\displaystyle S,T:C^{\mathrm {op} }\times C\to D,}$

written

${\displaystyle \alpha :S{\ddot {\to }}T,}$

is a function that to every object ${\displaystyle c}$ of ${\displaystyle C}$ associates an arrow

${\displaystyle \alpha _{c}:S(c,c)\to T(c,c)}$ of ${\displaystyle D}$

and satisfies the following coherence property: for every morphism ${\displaystyle f:c\to c'}$ of ${\displaystyle C}$ the diagram

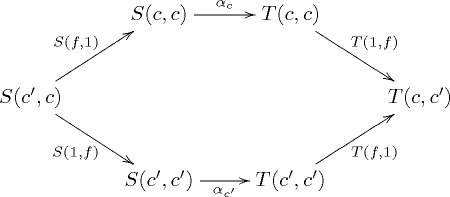
commutes.^[1] Note the direction of ${\displaystyle S(f,g)}$ is opposite along ${\displaystyle f}$ in the first component since it is contravariant.

The composition of two dinatural transformations need not be dinatural.

See also

• Extranatural transformation
• Natural transformation

Notes

1. Mac Lane, Saunders (2013). Categories for the working mathematician. Springer Science & Business Media. p. 218.

References

• Fosco, Loregian (22 July 2021), (Co)end Calculus, Cambridge University Press, arXiv:1501.02503, doi:10.1017/9781108778657, ISBN 9781108746120, S2CID 237839003
• Dubuc, Eduardo; Street, Ross (1970). "Dinatural transformations". Reports of the Midwest Category Seminar IV. Lecture Notes in Mathematics. Vol. 137. pp. 126–137. doi:10.1007/BFb0060443. ISBN 978-3-540-04926-5.

External links

• dinatural transformation at the nLab