Semi-continuity

For the notion of upper or lower semi-continuous set-valued function, see Hemicontinuity.

In mathematical analysis, semicontinuity (or semi-continuity) is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function ${\displaystyle f}$ is upper (respectively, lower) semicontinuous at a point ${\displaystyle x_{0}}$ if, roughly speaking, the function values for arguments near ${\displaystyle x_{0}}$ are not much higher (respectively, lower) than ${\displaystyle f\left(x_{0}\right).}$ Briefly, a function on a ___domain ${\displaystyle X}$ is lower semi-continuous if its epigraph ${\displaystyle \{(x,t)\in X\times \mathbb {R} :t\geq f(x)\}}$ is closed in ${\displaystyle X\times \mathbb {R} }$, and upper semi-continuous if ${\displaystyle -f}$ is lower semi-continuous.

An upper semicontinuous function that is not lower semicontinuous at ${\displaystyle x_{0}}$. The solid blue dot indicates ${\displaystyle f\left(x_{0}\right).}$

A lower semicontinuous function that is not upper semicontinuous at ${\displaystyle x_{0}}$. The solid blue dot indicates ${\displaystyle f\left(x_{0}\right).}$

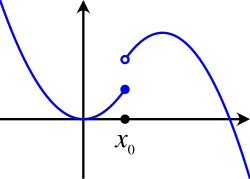
A function is continuous if and only if it is both upper and lower semicontinuous. If we take a continuous function and increase its value at a certain point ${\displaystyle x_{0}}$ to ${\displaystyle f\left(x_{0}\right)+c}$ for some ${\displaystyle c>0}$, then the result is upper semicontinuous; if we decrease its value to ${\displaystyle f\left(x_{0}\right)-c}$ then the result is lower semicontinuous.

The notion of upper and lower semicontinuous function was first introduced and studied by René Baire in his thesis in 1899.^[1]

Definitions

Assume throughout that ${\displaystyle X}$  is a topological space and ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is a function with values in the extended real numbers ${\displaystyle {\overline {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,\infty \}=[-\infty ,\infty ]}$ .

Upper semicontinuity

A function ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is called upper semicontinuous at a point ${\displaystyle x_{0}\in X}$  if for every real ${\displaystyle y>f\left(x_{0}\right)}$  there exists a neighborhood ${\displaystyle U}$  of ${\displaystyle x_{0}}$  such that ${\displaystyle f(x)<y}$  for all ${\displaystyle x\in U}$ .^[2] Equivalently, ${\displaystyle f}$  is upper semicontinuous at ${\displaystyle x_{0}}$  if and only if $${\displaystyle \limsup _{x\to x_{0}}f(x)\leq f(x_{0})}$$  where lim sup is the limit superior of the function ${\displaystyle f}$  at the point ${\displaystyle x_{0}.}$  Here the limit superior is defined as $${\displaystyle \inf _{U\ni x_{0}}\sup _{x\in U}f(x)}$$  where the supremum is taken over all neighborhoods of ${\displaystyle y}$ .

If ${\displaystyle X}$  is a metric space with distance function ${\displaystyle d}$  and ${\displaystyle f(x_{0})\in \mathbb {R} ,}$  this can also be restated using an ${\displaystyle \varepsilon }$ -${\displaystyle \delta }$  formulation, similar to the definition of continuous function. Namely, for each ${\displaystyle \varepsilon >0}$  there is a ${\displaystyle \delta >0}$  such that ${\displaystyle f(x)<f(x_{0})+\varepsilon }$  whenever ${\displaystyle d(x,x_{0})<\delta .}$ 

A function ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is called upper semicontinuous if it satisfies any of the following equivalent conditions:^[2]

(1) The function is upper semicontinuous at every point of its ___domain.

(2) For each ${\displaystyle y\in \mathbb {R} }$ , the set ${\displaystyle f^{-1}([-\infty ,y))=\{x\in X:f(x)<y\}}$  is open in ${\displaystyle X}$ , where ${\displaystyle [-\infty ,y)=\{t\in {\overline {\mathbb {R} }}:t<y\}}$ .

(3) For each ${\displaystyle y\in \mathbb {R} }$ , the ${\displaystyle y}$ -superlevel set ${\displaystyle f^{-1}([y,\infty ))=\{x\in X:f(x)\geq y\}}$  is closed in ${\displaystyle X}$ .

(4) The hypograph ${\displaystyle \{(x,t)\in X\times \mathbb {R} :t\leq f(x)\}}$  is closed in ${\displaystyle X\times \mathbb {R} }$ .

(5) The function ${\displaystyle f}$  is continuous when the codomain ${\displaystyle {\overline {\mathbb {R} }}}$  is given the left order topology. This is just a restatement of condition (2) since the left order topology is generated by all the intervals ${\displaystyle [-\infty ,y)}$ .

Lower semicontinuity

A function ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is called lower semicontinuous at a point ${\displaystyle x_{0}\in X}$  if for every real ${\displaystyle y<f\left(x_{0}\right)}$  there exists a neighborhood ${\displaystyle U}$  of ${\displaystyle x_{0}}$  such that ${\displaystyle f(x)>y}$  for all ${\displaystyle x\in U}$ . Equivalently, ${\displaystyle f}$  is lower semicontinuous at ${\displaystyle x_{0}}$  if and only if $${\displaystyle \liminf _{x\to x_{0}}f(x)\geq f(x_{0})}$$  where ${\displaystyle \liminf }$  is the limit inferior of the function ${\displaystyle f}$  at point ${\displaystyle x_{0}.}$ 

If ${\displaystyle X}$  is a metric space with distance function ${\displaystyle d}$  and ${\displaystyle f(x_{0})\in \mathbb {R} ,}$  this can also be restated as follows: For each ${\displaystyle \varepsilon >0}$  there is a ${\displaystyle \delta >0}$  such that ${\displaystyle f(x)>f(x_{0})-\varepsilon }$  whenever ${\displaystyle d(x,x_{0})<\delta .}$ 

A function ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is called lower semicontinuous if it satisfies any of the following equivalent conditions:

(1) The function is lower semicontinuous at every point of its ___domain.

(2) For each ${\displaystyle y\in \mathbb {R} }$ , the set ${\displaystyle f^{-1}((y,\infty ])=\{x\in X:f(x)>y\}}$  is open in ${\displaystyle X}$ , where ${\displaystyle (y,\infty ]=\{t\in {\overline {\mathbb {R} }}:t>y\}}$ .

(3) For each ${\displaystyle y\in \mathbb {R} }$ , the ${\displaystyle y}$ -sublevel set ${\displaystyle f^{-1}((-\infty ,y])=\{x\in X:f(x)\leq y\}}$  is closed in ${\displaystyle X}$ .

(4) The epigraph ${\displaystyle \{(x,t)\in X\times \mathbb {R} :t\geq f(x)\}}$  is closed in ${\displaystyle X\times \mathbb {R} }$ .^[3]: 207

(5) The function ${\displaystyle f}$  is continuous when the codomain ${\displaystyle {\overline {\mathbb {R} }}}$  is given the right order topology. This is just a restatement of condition (2) since the right order topology is generated by all the intervals ${\displaystyle (y,\infty ]}$ .

Examples

Consider the function ${\displaystyle f,}$  piecewise defined by: $${\displaystyle f(x)={\begin{cases}-1&{\mbox{if }}x<0,\\1&{\mbox{if }}x\geq 0\end{cases}}}$$  This function is upper semicontinuous at ${\displaystyle x_{0}=0,}$  but not lower semicontinuous.

The floor function ${\displaystyle f(x)=\lfloor x\rfloor ,}$  which returns the greatest integer less than or equal to a given real number ${\displaystyle x,}$  is everywhere upper semicontinuous. Similarly, the ceiling function ${\displaystyle f(x)=\lceil x\rceil }$  is lower semicontinuous.

Upper and lower semicontinuity bear no relation to continuity from the left or from the right for functions of a real variable. Semicontinuity is defined in terms of an ordering in the range of the functions, not in the ___domain.^[4] For example the function $${\displaystyle f(x)={\begin{cases}\sin(1/x)&{\mbox{if }}x\neq 0,\\1&{\mbox{if }}x=0,\end{cases}}}$$  is upper semicontinuous at ${\displaystyle x=0}$  while the function limits from the left or right at zero do not even exist.

If ${\displaystyle X=\mathbb {R} ^{n}}$  is a Euclidean space (or more generally, a metric space) and ${\displaystyle \Gamma =C([0,1],X)}$  is the space of curves in ${\displaystyle X}$  (with the supremum distance ${\displaystyle d_{\Gamma }(\alpha ,\beta )=\sup\{d_{X}(\alpha (t),\beta (t)):t\in [0,1]\}}$ ), then the length functional ${\displaystyle L:\Gamma \to [0,+\infty ],}$  which assigns to each curve ${\displaystyle \alpha }$  its length ${\displaystyle L(\alpha ),}$  is lower semicontinuous.^[5] As an example, consider approximating the unit square diagonal by a staircase from below. The staircase always has length 2, while the diagonal line has only length ${\displaystyle {\sqrt {2}}}$ .

A fundamental example in real analysis is Fatou's lemma. It asserts that if ${\displaystyle f_{n}}$  is a sequence of non-negative measurable functions, then $${\displaystyle \int \liminf f_{n}\leq \liminf \int f_{n}}$$  where ${\displaystyle \liminf }$  denotes the (pointwise) limit inferior. What this means, in full generality, is that if ${\displaystyle (X,\mu )}$  be a measure space and ${\displaystyle L^{+}(X,\mu )}$  denotes the set of positive measurable functions endowed with the topology of convergence in measure with respect to ${\displaystyle \mu ,}$  then the integral, seen as an operator from ${\displaystyle L^{+}(X,\mu )}$  to ${\displaystyle [-\infty ,+\infty ]}$  is lower semicontinuous.

Properties

Unless specified otherwise, all functions below are from a topological space ${\displaystyle X}$  to the extended real numbers ${\displaystyle {\overline {\mathbb {R} }}=[-\infty ,\infty ].}$  Several of the results hold for semicontinuity at a specific point, but for brevity they are only stated for semicontinuity over the whole ___domain.

• A function ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is continuous if and only if it is both upper and lower semicontinuous.
• The characteristic function or indicator function of a set ${\displaystyle A\subset X}$  (defined by ${\displaystyle \mathbf {1} _{A}(x)=1}$  if ${\displaystyle x\in A}$  and ${\displaystyle 0}$  if ${\displaystyle x\notin A}$ ) is upper semicontinuous if and only if ${\displaystyle A}$  is a closed set. It is lower semicontinuous if and only if ${\displaystyle A}$  is an open set.
• In the field of convex analysis, the characteristic function of a set ${\displaystyle A\subset X}$  is defined differently, as ${\displaystyle \chi _{A}(x)=0}$  if ${\displaystyle x\in A}$  and ${\displaystyle \chi _{A}(x)=\infty }$  if ${\displaystyle x\notin A}$ . With that definition, the characteristic function of any closed set is lower semicontinuous, and the characteristic function of any open set is upper semicontinuous.

Binary operations on semicontinuous functions

Let ${\displaystyle f,g:X\to {\overline {\mathbb {R} }}}$ .

• If ${\displaystyle f}$  and ${\displaystyle g}$  are lower semicontinuous, then the sum ${\displaystyle f+g}$  is lower semicontinuous^[6] (provided the sum is well-defined, i.e., ${\displaystyle f(x)+g(x)}$  is not the indeterminate form ${\displaystyle -\infty +\infty }$ ). The same holds for upper semicontinuous functions.
• If ${\displaystyle f}$  and ${\displaystyle g}$  are lower semicontinuous and non-negative, then the product function ${\displaystyle fg}$  is lower semicontinuous. The corresponding result holds for upper semicontinuous functions.
• The function ${\displaystyle f}$  is lower semicontinuous if and only if ${\displaystyle -f}$  is upper semicontinuous.
• If ${\displaystyle f}$  and ${\displaystyle g}$  are upper semicontinuous and ${\displaystyle f}$  is non-decreasing, then the composition ${\displaystyle f\circ g}$  is upper semicontinuous. On the other hand, if ${\displaystyle f}$  is not non-decreasing, then ${\displaystyle f\circ g}$  may not be upper semicontinuous. For example take ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$  defined as ${\displaystyle f(x)=-x}$ . Then ${\displaystyle f}$  is continuous and ${\displaystyle f\circ g=-g}$ , which is not upper semicontinuous unless ${\displaystyle g}$  is continuous.
• If ${\displaystyle f}$  and ${\displaystyle g}$  are lower semicontinuous, their (pointwise) maximum and minimum (defined by ${\displaystyle x\mapsto \max\{f(x),g(x)\}}$  and ${\displaystyle x\mapsto \min\{f(x),g(x)\}}$ ) are also lower semicontinuous. Consequently, the set of all lower semicontinuous functions from ${\displaystyle X}$  to ${\displaystyle {\overline {\mathbb {R} }}}$  (or to ${\displaystyle \mathbb {R} }$ ) forms a lattice. The corresponding statements also hold for upper semicontinuous functions.

Optimization of semicontinuous functions

• The (pointwise) supremum of an arbitrary family ${\displaystyle (f_{i})_{i\in I}}$  of lower semicontinuous functions ${\displaystyle f_{i}:X\to {\overline {\mathbb {R} }}}$  (defined by ${\displaystyle f(x)=\sup\{f_{i}(x):i\in I\}}$ ) is lower semicontinuous.^[7]

In particular, the limit of a monotone increasing sequence ${\displaystyle f_{1}\leq f_{2}\leq f_{3}\leq \cdots }$  of continuous functions is lower semicontinuous. (The Theorem of Baire below provides a partial converse.) The limit function will only be lower semicontinuous in general, not continuous. An example is given by the functions ${\displaystyle f_{n}(x)=1-(1-x)^{n}}$  defined for ${\displaystyle x\in [0,1]}$  for ${\displaystyle n=1,2,\ldots .}$ 

Likewise, the infimum of an arbitrary family of upper semicontinuous functions is upper semicontinuous. And the limit of a monotone decreasing sequence of continuous functions is upper semicontinuous.

• If ${\displaystyle C}$  is a compact space (for instance a closed bounded interval ${\displaystyle [a,b]}$ ) and ${\displaystyle f:C\to {\overline {\mathbb {R} }}}$  is upper semicontinuous, then ${\displaystyle f}$  attains a maximum on ${\displaystyle C.}$  If ${\displaystyle f}$  is lower semicontinuous on ${\displaystyle C,}$  it attains a minimum on ${\displaystyle C.}$ 

(Proof for the upper semicontinuous case: By condition (5) in the definition, ${\displaystyle f}$  is continuous when ${\displaystyle {\overline {\mathbb {R} }}}$  is given the left order topology. So its image ${\displaystyle f(C)}$  is compact in that topology. And the compact sets in that topology are exactly the sets with a maximum. For an alternative proof, see the article on the extreme value theorem.)

Other properties

• (Theorem of Baire)^{[note 1]} Let ${\displaystyle X}$  be a metric space. Every lower semicontinuous function ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is the limit of a point-wise increasing sequence of extended real-valued continuous functions on ${\displaystyle X.}$  In particular, there exists a sequence ${\displaystyle \{f_{i}\}}$  of continuous functions ${\displaystyle f_{i}:X\to {\overline {\mathbb {R} }}}$  such that

$${\displaystyle f_{i}(x)\leq f_{i+1}(x)\quad \forall x\in X,\ \forall i=0,1,2,\dots }$$  and

$${\displaystyle \lim _{i\to \infty }f_{i}(x)=f(x)\quad \forall x\in X.}$$ 

If ${\displaystyle f}$  does not take the value ${\displaystyle -\infty }$ , the continuous functions can be taken to be real-valued.^[8][9]

Additionally, every upper semicontinuous function ${\displaystyle f:X\to {\overline {\mathbb {R} }}}$  is the limit of a monotone decreasing sequence of extended real-valued continuous functions on ${\displaystyle X;}$  if ${\displaystyle f}$  does not take the value ${\displaystyle \infty ,}$  the continuous functions can be taken to be real-valued.

• Any upper semicontinuous function ${\displaystyle f:X\to \mathbb {N} }$  on an arbitrary topological space ${\displaystyle X}$  is locally constant on some dense open subset of ${\displaystyle X.}$ 

• If the topological space ${\displaystyle X}$  is sequential, then ${\displaystyle f:X\to \mathbb {R} }$  is upper semi-continuous if and only if it is sequentially upper semi-continuous, that is, if for any ${\displaystyle x\in X}$  and any sequence ${\displaystyle (x_{n})_{n}\subset X}$  that converges towards ${\displaystyle x}$ , there holds ${\displaystyle \limsup _{n\to \infty }f(x_{n})\leqslant f(x)}$ . Equivalently, in a sequential space, ${\displaystyle f}$  is upper semicontinuous if and only if its superlevel sets ${\displaystyle \{\,x\in X\,|\,f(x)\geqslant y\,\}}$  are sequentially closed for all ${\displaystyle y\in \mathbb {R} }$ . In general, upper semicontinuous functions are sequentially upper semicontinuous, but the converse may be false.

Semicontinuity of set-valued functions

For set-valued functions, several concepts of semicontinuity have been defined, namely upper, lower, outer, and inner semicontinuity, as well as upper and lower hemicontinuity. A set-valued function ${\displaystyle F}$  from a set ${\displaystyle A}$  to a set ${\displaystyle B}$  is written ${\displaystyle F:A\rightrightarrows B.}$  For each ${\displaystyle x\in A,}$  the function ${\displaystyle F}$  defines a set ${\displaystyle F(x)\subset B.}$  The preimage of a set ${\displaystyle S\subset B}$  under ${\displaystyle F}$  is defined as $${\displaystyle F^{-1}(S):=\{x\in A:F(x)\cap S\neq \varnothing \}.}$$  That is, ${\displaystyle F^{-1}(S)}$  is the set that contains every point ${\displaystyle x}$  in ${\displaystyle A}$  such that ${\displaystyle F(x)}$  is not disjoint from ${\displaystyle S}$ .^[10]

Upper and lower semicontinuity

A set-valued map ${\displaystyle F:\mathbb {R} ^{m}\rightrightarrows \mathbb {R} ^{n}}$  is upper semicontinuous at ${\displaystyle x\in \mathbb {R} ^{m}}$  if for every open set ${\displaystyle U\subset \mathbb {R} ^{n}}$  such that ${\displaystyle F(x)\subset U}$ , there exists a neighborhood ${\displaystyle V}$  of ${\displaystyle x}$  such that ${\displaystyle F(V)\subset U.}$ ^{[10]: Def. 2.1}

A set-valued map ${\displaystyle F:\mathbb {R} ^{m}\rightrightarrows \mathbb {R} ^{n}}$  is lower semicontinuous at ${\displaystyle x\in \mathbb {R} ^{m}}$  if for every open set ${\displaystyle U\subset \mathbb {R} ^{n}}$  such that ${\displaystyle x\in F^{-1}(U),}$  there exists a neighborhood ${\displaystyle V}$  of ${\displaystyle x}$  such that ${\displaystyle V\subset F^{-1}(U).}$ ^{[10]: Def. 2.2}

Upper and lower set-valued semicontinuity are also defined more generally for a set-valued maps between topological spaces by replacing ${\displaystyle \mathbb {R} ^{m}}$  and ${\displaystyle \mathbb {R} ^{n}}$  in the above definitions with arbitrary topological spaces.^[10]

Note, that there is not a direct correspondence between single-valued lower and upper semicontinuity and set-valued lower and upper semicontinuouty. An upper semicontinuous single-valued function is not necessarily upper semicontinuous when considered as a set-valued map.^[10]: 18 For example, the function ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$  defined by $${\displaystyle f(x)={\begin{cases}-1&{\mbox{if }}x<0,\\1&{\mbox{if }}x\geq 0\end{cases}}}$$  is upper semicontinuous in the single-valued sense but the set-valued map ${\displaystyle x\mapsto F(x):=\{f(x)\}}$  is not upper semicontinuous in the set-valued sense.

Inner and outer semicontinuity

A set-valued function ${\displaystyle F:\mathbb {R} ^{m}\rightrightarrows \mathbb {R} ^{n}}$  is called inner semicontinuous at ${\displaystyle x}$  if for every ${\displaystyle y\in F(x)}$  and every convergent sequence ${\displaystyle (x_{i})}$  in ${\displaystyle \mathbb {R} ^{m}}$  such that ${\displaystyle x_{i}\to x}$ , there exists a sequence ${\displaystyle (y_{i})}$  in ${\displaystyle \mathbb {R} ^{n}}$  such that ${\displaystyle y_{i}\to y}$  and ${\displaystyle y_{i}\in F\left(x_{i}\right)}$  for all sufficiently large ${\displaystyle i\in \mathbb {N} .}$ ^{[11][note 2]}

A set-valued function ${\displaystyle F:\mathbb {R} ^{m}\rightrightarrows \mathbb {R} ^{n}}$  is called outer semicontinuous at ${\displaystyle x}$  if for every convergence sequence ${\displaystyle (x_{i})}$  in ${\displaystyle \mathbb {R} ^{m}}$  such that ${\displaystyle x_{i}\to x}$  and every convergent sequence ${\displaystyle (y_{i})}$  in ${\displaystyle \mathbb {R} ^{n}}$  such that ${\displaystyle y_{i}\in F(x_{i})}$  for each ${\displaystyle i\in \mathbb {N} ,}$  the sequence ${\displaystyle (y_{i})}$  converges to a point in ${\displaystyle F(x)}$  (that is, ${\displaystyle \lim _{i\to \infty }y_{i}\in F(x)}$ ).^[11]

Hulls

Because the supremum of a family of lower semicontinuous functions is lower semicontinuous, if ${\displaystyle f}$  is an arbitrary extended-real valued function on a topological space ${\displaystyle X}$ , the supremum of the set of lower semicontinuous functions majorized by ${\displaystyle f}$  is lower semicontinuous. This greatest lower semicontinuous function majorized by ${\displaystyle f}$  is the lower semicontinuous hull of ${\displaystyle f}$ .^[12] The hull ${\displaystyle H_{f}}$  is defined pointwise by the relation^[13] $${\displaystyle H_{f}(x)=\liminf _{y\to x}f(y).}$$  The hull ${\displaystyle H_{f}}$  has the property that its epigraph is the closure of the epigraph of ${\displaystyle f}$ .

The lower semicontinuous hull plays a role in convex analysis. Given a convex (extended real) function, the epigraph might not be closed. But the lower semicontinuous hull of a convex function is convex, and is known as the closure of the original convex function.

Some operations in convex analysis, such as the Legendre transform automatically produce closed convex functions. The Legendre transform applied twice to a convex function gives the closure of the original function, rather than the original function. Thus the lower semicontinuous hull is a way of regularizing convex functions, by modifying it at boundary points of its effective ___domain.

In categorical terms, the lower semicontinuous hull of a function ${\displaystyle f}$  is the (left) Kan extension of ${\displaystyle f}$  along the inclusion of the poset of open neighborhoods (ordered by reverse inclusion) into the topological space ${\displaystyle X}$ . Explicitly, the value of the hull ${\displaystyle H_{f}}$  at a point ${\displaystyle x\in X}$  is given by the colimit: $${\displaystyle (\mathrm {Lan} _{\iota }f)(x)=\inf _{U\ni x}\sup _{y\in U}f(y),}$$  which coincides with ${\displaystyle \liminf _{y\to x}f(y)}$ , the left Kan extension under the inclusion functor ${\displaystyle \iota }$ . In this formulation, the process of taking the semicontinuous envelope is a special case of the Kan extension machinery in enriched category theory. The upper semicontinuous hull is a right Kan extension.^{[citation needed]}

Other types of hulls are often considered in applications. For example, the infimum of the set of continuous affine functions that majorize a given function on a convex subset of a topological vector space is upper semicontinuous. This fact is used in the proof of the Choquet theorem.^[14] Similar ideas applied to subharmonic functions are used in the Perron method for solving the Dirichlet problem for the Laplace operator in a ___domain. The key condition for the class of subharmonic solutions is upper semicontinuity, particularly near the boundary where the boundary conditions are applied.

Applications

Calculus of variations

Main article: Direct methods in the calculus of variations

An important application of semicontinuity is to the calculus of variations. It derives its significance in this context due to the following theorem.^[15] Let ${\displaystyle X}$  be a topological space, and ${\displaystyle F:X\to (-\infty ,+\infty ]}$ . A minimizing sequence is a sequence ${\displaystyle x_{k}}$  in ${\displaystyle X}$  such that $${\displaystyle \lim _{k\to \infty }F(x_{k})=\inf _{X}F.}$$  The theorem is that if ${\displaystyle F}$  is sequentially lower semicontinuous and ${\displaystyle x_{k}}$  is a minimizing sequence that converges to ${\displaystyle x_{0}}$ , then $${\displaystyle F(x_{0})=\inf _{X}F.}$$  That is, ${\displaystyle x_{0}}$  is an absolute minimum of ${\displaystyle F}$ .

This is often combined with results such as Tonelli's theorem in functional analysis, which characterizes the weak lower semicontinuity of nonlinear functionals on L^p spaces in terms of the convexity of another function. More specialized results of this kind are useful in variational formulations of problems in partial differential equations, which relate semicontinuity of functionals given by integration to the convexity properties of the integrand, often defined on some Sobolev space. The prototypical example is the Dirichlet problem for the Laplace operator, which can be formulated as a minimization problem of the energy, subject to boundary conditions, $${\displaystyle F(u)=\int _{\Omega }|\nabla u|^{2},}$$  i.e., the integral of the squared norm of the gradient of a function over a bounded ___domain in Euclidean space. The integrand is convex in an appropriate Sobolev space, so the limit of a minimizing sequence is a solution of the Dirichlet problem. This has implications, for instance, for finite element solutions, which gives a way to construct a minimizing sequence.

Existence of saddle points

Together with convexity assumptions, both upper and lower semicontinuity play a role in theorems guaranteeing the existence of saddle points of functions, on locally convex topological vector spaces. One such result is the minimax theorem of Fan and Sion.^[16] It states that if ${\displaystyle f:X\times Y\to \mathbb {R} }$  is a function from a pair of non-empty closed, convex sets ${\displaystyle X,Y}$  belonging to reflexive Banach spaces, such that

• ${\displaystyle f(x,\cdot )}$  is concave and upper semicontinuous for each ${\displaystyle x\in X}$  and
• ${\displaystyle f(\cdot ,y)}$  is convex and lower semicontinuous for each ${\displaystyle y\in Y}$ ,

then the set of saddle points of ${\displaystyle f}$  is convex. If both convexity and concavity are strict, then there is at most one saddle point. If the sets ${\displaystyle X}$  and ${\displaystyle Y}$  are bounded, then the set of saddle points is non-empty. A saddle point is by definition a point ${\displaystyle (x_{0},y_{0})}$  at which $${\displaystyle f(x_{0},y_{0})=\inf _{x\in X}\sup _{y\in Y}f(x,y)=\sup _{y\in Y}\inf _{x\in X}f(x,y).}$$ 

Dimension

 

Illustration of the face-dimension function ${\displaystyle f}$  on a hexagon in the plane

Many integer-valued functions of importance are also semicontinuous. For a simple example, suppose one has a polyhedron ${\displaystyle K}$  (or, more generally, a closed convex set) in an ${\displaystyle n}$ -dimensional vector space. A face of ${\displaystyle K}$  is by definition the set of maxima of some linear functional on ${\displaystyle K}$ . Define the function $${\displaystyle f(x)=\inf\{\dim F|F{\text{ is a face of }}K{\text{ and }}x\in F\}.}$$  Then ${\displaystyle f}$  is lower semicontinuous. This is intuitively because under any small perturbations, you can move from a face of lower dimension, such as an edge or vertex, to one of higher dimension, but any point of a higher dimensional face cannot be moved to one of lower dimension if the perturbation is small enough.

Another example of a similar character is that matrix rank is a lower semicontinuous function on the space of ${\displaystyle n\times m}$  matrices. This is because the rank can go up at matrices which are nearby, but not down. As a result of this, together with the implicit function theorem, when a Lie group acts smoothly on a smooth manifold, the dimension of the orbit through a point is lower semicontinuous (i.e., the function ${\displaystyle f(x)=\dim(G\cdot x)}$ ).^[17]

Algebraic geometry

See also: Semicontinuity theorem

More sophisticated versions of this same idea play a fundamental role in algebraic geometry, where many dimension maps with codomain in the integers are known to be semicontinuous. (For example as applied to a Newton–Okounkov body.)

In general, let ${\displaystyle X}$  and ${\displaystyle S}$  be schemes and ${\displaystyle f:X\to S}$  a flat and proper morphism of finite presentation. Let ${\displaystyle {\mathcal {F}}}$  be an ${\displaystyle {\mathcal {O}}_{X}}$ -module flat and of finite presentation over ${\displaystyle S}$ . Then for any ${\displaystyle i\in \mathbb {Z} }$  the function $${\displaystyle h^{i}:S\to \mathbb {Z} _{\geq 0},s\mapsto {\text{dim}}_{\kappa (s)}H^{i}(X_{s},{\mathcal {F}}_{s})}$$  is upper semicontinuous.^[18] An important special case of this theorem when additionally ${\displaystyle X,S}$  are noetherian, ${\displaystyle f}$  is projective and ${\displaystyle {\mathcal {F}}}$  is coherent can be found in the standard textbook of Hartshorne.^[19]: 288 Original work in the language of hypercohomology can be found in EGA III^[20] Théorème (7.7.5), citing also previous work, in particular Grauert for the complex-analytic setting.

Let ${\displaystyle X,Y}$  be schemes and ${\displaystyle f:X\to Y}$  a morphism of finite type. The function $${\displaystyle n_{X/Y}:Y\to \mathbb {Z} _{\geq 0}\cup \{\infty \},y\mapsto {\text{dim}}_{\text{top}}X_{y}}$$  associates to any ${\displaystyle y\in Y}$  the dimension of the fiber ${\displaystyle X_{y}}$ . If ${\displaystyle f}$  is a flat morphism of schemes of finite presentation, then ${\displaystyle n_{X/Y}}$  is lower semicontinuous.^[21] If ${\displaystyle f}$  is a proper morphism of schemes, then ${\displaystyle n_{X/Y}}$  is upper semicontinuous.^[22]

Vakil collected a list of further semicontinuity results in algebraic geometry.^[23]

Descriptive set theory

Main article: Wadge hierarchy

Semicontinuous functions are used in descriptive set theory to define stratifications of topological spaces by complexity measures such as dimension, rank, or ordinal height.^[24][25][26] Such functions often take values in an ordinal, and their semicontinuity ensures that the sets ${\displaystyle \{x:f(x)\geq \alpha \}}$  are closed (and hence Borel in a Polish space).

A central example is the rank function on well-founded trees. Let ${\displaystyle {\mathcal {T}}\subseteq \omega ^{<\omega }}$  be a tree coded by a point in Baire space ${\displaystyle \omega ^{\omega }}$ . The rank ${\displaystyle \rho ({\mathcal {T}})\in \omega _{1}\cup \{\infty \}}$  is defined as the supremum of the lengths of descending sequences in ${\displaystyle {\mathcal {T}}}$ . The function assigning the rank ${\displaystyle \rho ({\mathcal {T}})}$  to each tree is lower semicontinuous with respect to the natural topology on tree codes. This rank stratifies the space of trees into closed sets ${\displaystyle \{{\mathcal {T}}:\rho ({\mathcal {T}})\geq \alpha \}}$ , analogous to how matrix rank stratifies ${\displaystyle \mathbb {R} ^{n\times m}}$ .

More generally, ordinal-valued lower semicontinuous functions are used to measure the complexity of points or structures in a Polish space—such as Scott ranks of countable structures, projective ranks of sets, or Lusin–Novikov complexities of equivalence relations. These functions enable fine classification and are crucial in defining universal sets and effective parametrizations in higher levels of the projective hierarchy.

Because the preimage of an interval ${\displaystyle [\alpha ,\infty ]}$  under a lower semicontinuous function is closed, such functions yield canonical stratifications of topological spaces into closed (thus Borel) pieces of increasing complexity. This property is often used in proofs of reflection principles, separation theorems, and in the effective classification of Borel equivalence relations.

Dynamical systems

Main articles: Entropy (information theory) and Invariant measure

In ergodic theory and topological dynamics, semicontinuity arises naturally when studying functionals on the space of invariant measures of a dynamical system. The most important example is the entropy function, which assigns to each invariant measure its measure-theoretic entropy.^[27][28][29]

Let ${\displaystyle (X,T)}$  be a topological dynamical system with ${\displaystyle X}$  compact and ${\displaystyle T:X\to X}$  continuous. The space ${\displaystyle {\mathcal {M}}_{T}(X)}$  of ${\displaystyle T}$ -invariant Borel probability measures is a compact convex subset of the dual of ${\displaystyle C(X)}$  under the weak-* topology. The entropy map ${\displaystyle \mu \mapsto h_{\mu }(T)}$  is an upper semicontinuous function on ${\displaystyle {\mathcal {M}}_{T}(X)}$ : $${\displaystyle \limsup _{\mu _{n}\to \mu }h_{\mu _{n}}(T)\leq h_{\mu }(T).}$$ 

This property plays a key role in the variational principle, which asserts that the topological entropy ${\displaystyle h_{\mathrm {top} }(T)}$  is the supremum of ${\displaystyle h_{\mu }(T)}$  over all invariant measures. Upper semicontinuity guarantees that this supremum is attained when the space of measures is compact.

More generally, many functionals of interest—such as Lyapunov exponents, dimension spectra, or return time statistics—are semicontinuous on the space of invariant measures. In some cases, these semicontinuity properties are used to prove existence of measures maximizing or minimizing a given quantity, or to establish structural properties of the simplex ${\displaystyle {\mathcal {M}}_{T}(X)}$  (e.g., that ergodic measures form a residual—dense ${\displaystyle G_{\delta }}$ —set).

Similar ideas appear in the theory of joinings, where one studies invariant couplings between systems. The set of joinings is compact in the weak-* topology, and semicontinuity is used to analyze disjointness and uniqueness of invariant couplings.

See also

• Directional continuity – Mathematical function with no sudden changesPages displaying short descriptions of redirect targets
• Katětov–Tong insertion theorem – On existence of a continuous function between semicontinuous upper and lower bounds
• Hemicontinuity – Semicontinuity for set-valued functions
• Càdlàg – Right continuous function with left limits

Notes

1. The result was proved by René Baire in 1904 for real-valued function defined on ${\displaystyle \mathbb {R} }$ . It was extended to metric spaces by Hans Hahn in 1917, and Hing Tong showed in 1952 that the most general class of spaces where the theorem holds is the class of perfectly normal spaces. (See Engelking, Exercise 1.7.15(c), p. 62 for details and specific references.)
2. In particular, there exists ${\displaystyle i_{0}\geq 0}$  such that ${\displaystyle y_{i}\in F(x_{i})}$  for every natural number ${\displaystyle i\geq i_{0},}$ . The necessisty of only considering the tail of ${\displaystyle y_{i}}$  comes from the fact that for small values of ${\displaystyle i,}$  the set ${\displaystyle F(x_{i})}$  may be empty.

References

1. Verry, Matthieu. "Histoire des mathématiques - René Baire".
2. Stromberg, p. 132, Exercise 4
3. Kurdila, A. J., Zabarankin, M. (2005). "Lower Semicontinuous Functionals". Convex Functional Analysis. Systems & Control: Foundations & Applications (1st ed.). Birkhäuser-Verlag. pp. 205–219. doi:10.1007/3-7643-7357-1_7. ISBN 978-3-7643-2198-7.
4. Willard, p. 49, problem 7K
5. Giaquinta, Mariano (2007). Mathematical analysis : linear and metric structures and continuity. Giuseppe Modica (1 ed.). Boston: Birkhäuser. Theorem 11.3, p.396. ISBN 978-0-8176-4514-4. OCLC 213079540.
6. Puterman, Martin L. (2005). Markov Decision Processes Discrete Stochastic Dynamic Programming. Wiley-Interscience. pp. 602. ISBN 978-0-471-72782-8.
7. "To show that the supremum of any collection of lower semicontinuous functions is lower semicontinuous".
8. Stromberg, p. 132, Exercise 4(g)
9. "Show that lower semicontinuous function is the supremum of an increasing sequence of continuous functions".
10. Freeman, R. A., Kokotović, P. (1996). Robust Nonlinear Control Design. Birkhäuser Boston. doi:10.1007/978-0-8176-4759-9. ISBN 978-0-8176-4758-2..
11. Goebel, R. K. (January 2024). "Chapter 2: Set convergence and set-valued mappings". Set-Valued, Convex, and Nonsmooth Analysis in Dynamics and Control: An Introduction. Other Titles in Applied Mathematics. Society for Industrial and Applied Mathematics. pp. 21–36. doi:10.1137/1.9781611977981.ch2. ISBN 978-1-61197-797-4.
12. Rockafellar 1970.
13. Bourbaki 1966, IV.6.2. sfn error: no target: CITEREFBourbaki1966 (help)
14. Phelps 1966, Chapter 3.
15. Giusti 2003.
16. Ekeland & Témam 1999, Chapter 4.
17. Alexandrino, M. M. and Bettiol, R. G.(2015). Proper and isometric group actions. In Lecture Notes of the Unione Matematica Italiana (Vol. 23, pp. 51-84). Springer.
18. "Stacks Project — Lemma 36.32.1". Stacks.math.columbia.edu. Retrieved 2025-04-27.
19. Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157, Zbl 0367.14001, Ch. III Theorem 12.8
20. Grothendieck, Alexandre; Dieudonné, Jean (1963). "Éléments de géométrie algébrique: III. Étude cohomologique des faisceaux cohérents, Seconde partie". Publications Mathématiques de l'IHÉS. 17: 67. doi:10.1007/bf02684890. MR 0163911.
21. "Stacks Project — Lemma 37.30.4". Stacks.math.columbia.edu. Retrieved 2025-04-27.
22. "Stacks Project — Lemma 37.30.5". Stacks.math.columbia.edu. Retrieved 2025-04-27.
23. Ravi D., Vakil (2011-06-08). "Favorite semicontinuous functions?". math216.wordpress.com. Stanford University: Wordpress. Retrieved 2025-04-27.
24. Kechris, A. S. (1995). Classical Descriptive Set Theory. Springer.
25. Moschovakis, Y. N. (1980). Descriptive Set Theory. North-Holland.
26. Friedman, H., & Stanley, L. (1989). A Borel reducibility theory for classes of countable structures. J. Symbolic Logic, 54(3), 894–914.
27. Walters, P. (1982). An Introduction to Ergodic Theory. Springer.
28. Glasner, E. (2003). Ergodic Theory via Joinings. American Mathematical Society.
29. Downarowicz, T. (2011). Entropy in Dynamical Systems. Cambridge University Press.

Bibliography

• Benesova, B.; Kruzik, M. (2017). "Weak Lower Semicontinuity of Integral Functionals and Applications". SIAM Review. 59 (4): 703–766. arXiv:1601.00390. doi:10.1137/16M1060947. S2CID 119668631.
• Bourbaki, Nicolas (1998). Elements of Mathematics: General Topology, 1–4. Springer. ISBN 0-201-00636-7.
• Bourbaki, Nicolas (1998). Elements of Mathematics: General Topology, 5–10. Springer. ISBN 3-540-64563-2.
• Ekeland; Témam (1999), Convex analysis and variational problems
• Engelking, Ryszard (1989). General Topology. Heldermann Verlag, Berlin. ISBN 3-88538-006-4.
• Gelbaum, Bernard R.; Olmsted, John M.H. (2003). Counterexamples in analysis. Dover Publications. ISBN 0-486-42875-3.
• Giusti (2003), Direct methods in the calculus of variations
• Hyers, Donald H.; Isac, George; Rassias, Themistocles M. (1997). Topics in nonlinear analysis & applications. World Scientific. ISBN 981-02-2534-2.
• Rockafellar (1970), Convex analysis
• Rockafellar; Wets (1997), Variational analysis
• Phelps (1966), Lectures on the Choquet theorem
• Stromberg, Karl (1981). Introduction to Classical Real Analysis. Wadsworth. ISBN 978-0-534-98012-2.
• Willard, Stephen (2004) [1970]. General Topology. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.
• Zălinescu, Constantin (30 July 2002). Convex Analysis in General Vector Spaces. River Edge, N.J. London: World Scientific Publishing. ISBN 978-981-4488-15-0. MR 1921556. OCLC 285163112 – via Internet Archive.